|
Краткий теоретический
материал
2.
КОРПУСКУЛЯРНЫЕ СВОЙСТВА ЭЛЕКТРОМАГНИТНОГО
ИЗЛУЧЕНИЯ
3. МОДЕЛЬ АТОМА
РЕЗЕРФОРДА - БОРА
4.ВОЛНОВЫЕ
СВОЙСТВА ЧАСТИЦ. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
ГЕЙЗЕНБЕРГА
5. ЭЛЕМЕНТЫ
КВАНТОВОЙ МЕХАНИКИ
6. ЭЛЕКТРОННАЯ
ОБОЛОЧКА АТОМА. МОЛЕКУЛЯРНЫЕ СПЕКТРЫ
7.
РЕНТГЕНОВСКОЕ ИЗЛУЧЕНИЕ
8. СТРОЕНИЕ
АТОМНОГО ЯДРА. ДЕФЕКТ МАССЫ. ЭНЕРГИЯ СВЯЗИ ЯДРА. ЯДЕРНЫЕ
РЕАКЦИИ
9. ЕСТЕСТВЕННАЯ
РАДИОАКТИВНОСТЬ
Интегральная излучающая способность (или светимость)
абсолютно черного тела (АЧТ) определяется согласно закону
Стефана-Больцмана:
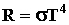 , где T -
абсолютная температура, s - постоянная Стефана -
Больцмана. Светимость теплового излучения серых тел: , где T -
абсолютная температура, s - постоянная Стефана -
Больцмана. Светимость теплового излучения серых тел:
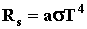 , где a -
поглощательная способность серого тела (коэффициент
серости). Первый закон Вина: , где a -
поглощательная способность серого тела (коэффициент
серости). Первый закон Вина: 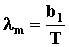 , где lm - длина волны, на которую приходится
максимум излучательной способности АЧТ, b1 =
2.886×10-3 (м×К) - первая постоянная Вина. Второй закон
Вина: , где lm - длина волны, на которую приходится
максимум излучательной способности АЧТ, b1 =
2.886×10-3 (м×К) - первая постоянная Вина. Второй закон
Вина: 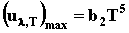 , где (ul,T)max - максимальное значение излучательной способности АЧТ,
b2 =
1.3×105 (Вт×м-3×К-5)- вторая постоянная Вина. Излучательная
способность АЧТ, являющаяся функцией температуры и длины
волны, вычисляется по формуле Планка: , где (ul,T)max - максимальное значение излучательной способности АЧТ,
b2 =
1.3×105 (Вт×м-3×К-5)- вторая постоянная Вина. Излучательная
способность АЧТ, являющаяся функцией температуры и длины
волны, вычисляется по формуле Планка: 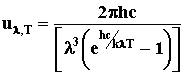 . .
Энергия светового кванта
определяется формулой: 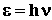 , где h =
6.625×10-34 Дж×с - постоянная Планка и n - частота света.
Масса фотона: , где h =
6.625×10-34 Дж×с - постоянная Планка и n - частота света.
Масса фотона: 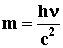 , где с - скорость
света в вакууме. Импульс фотона: , где с - скорость
света в вакууме. Импульс фотона: 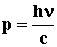 . Уравнение
Эйнштейна для внешнего фотоэффекта: . Уравнение
Эйнштейна для внешнего фотоэффекта: 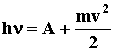 , где A - работа
выхода электрона из металла, m и v - масса и
скорость электрона. Если v = 0, hno = A, где nо - частота, соответствующая красной границе фотоэффекта.
Величина светового давления: , где A - работа
выхода электрона из металла, m и v - масса и
скорость электрона. Если v = 0, hno = A, где nо - частота, соответствующая красной границе фотоэффекта.
Величина светового давления: 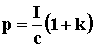 , где I -
количество энергии, падающей на единицу поверхности за единицу
времени, k - коэффициент отражения. Комптоновское
смещение длины волны рассеянного фотона: , где I -
количество энергии, падающей на единицу поверхности за единицу
времени, k - коэффициент отражения. Комптоновское
смещение длины волны рассеянного фотона: 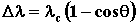 , где lс = 2.246×10-12 м - комптоновская длина волны
электрона. , где lс = 2.246×10-12 м - комптоновская длина волны
электрона.
Постулат Бора, определяющий условие стационарности
орбит (правило квантования орбит): m×vn×rn = n×h, где m - масса
электрона, n - номер орбиты (главное квантовое число: n = 1,
2, ...), vn
- скорость электрона на орбите радиуса rn, h = h/2p. Постулат Бора,
определяющий излучение и поглощение энергии (правило частот):
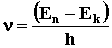 , где n - частота , где n - частота
излучения при переходе с n-ой на k-ю орбиту (n
> k),
En и Ek - энергия
электрона на этих орбитах. Частота излучения для
водородоподобных ионов (обобщенная формула Бальмера):
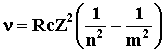 , где Z -
порядковый номер элемента, c - скорость света, , где Z -
порядковый номер элемента, c - скорость света, 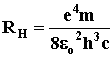 = 1.097×107 м-1 = 1.097×107 м-1
- постоянная Ридберга, e - заряд электрона, eo =
8.85×10-12
(Ф×м) - электрическая
постоянная.
Длина волны, соответствующая
микрочастице, движущейся со скоростью v (волна де
Бройля): lБ = h/mv, где
m – масса
частицы.
Соотношение де Бройля для энергии и
импульса частицы: E = hwБ, p =
hk, где wБ = 2pnБ - частота дебройлевской
волны, k = 2p/lБ - волновое
число.
Соотношения неопределенностей
Гейзенберга:
Dx×Dpx × h,
Dy×Dpy × h,
Dz×Dpz × h
,
где Dpx, Dpy, Dpz - интервалы, в которых
заключены проекции импульса частицы по осям x, y,
z.
5.
ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ.
Временное и стационарное уравнения
Шредингера: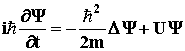 , ,  , где Y = Y(x, y, z, t) - , где Y = Y(x, y, z, t) -
полная волновая функция,
y = y(x, y, z) - ее координатная
часть, D - оператор Лапласа,
E и U - полная и потенциальная энергия, m
- масса частицы. Энергия микрочастицы в бесконечно глубокой
одномерной потенциальной яме: 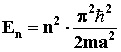 , где m –
масса микрочастицы, a – ширина ямы,
n = 1, 2, 3, … - квантовое число.
Волновая функция микрочастицы в яме: , где m –
масса микрочастицы, a – ширина ямы,
n = 1, 2, 3, … - квантовое число.
Волновая функция микрочастицы в яме: 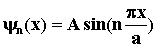 . Расстояние между
соседними уровнями энергии для микрочастицы, находящейся в
бесконечно глубокой одномерной потенциальной яме: . Расстояние между
соседними уровнями энергии для микрочастицы, находящейся в
бесконечно глубокой одномерной потенциальной яме: 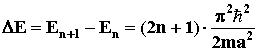 . Вероятность пребывания
частицы в разных местах ямы: . Вероятность пребывания
частицы в разных местах ямы: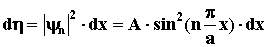 . .
Коэффициент прозрачности D потенциального барьера U(x):
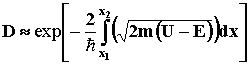 , где x1 и x2 – координаты точек, между которыми U>E. , где x1 и x2 – координаты точек, между которыми U>E.
Принцип Паули: в любой квантовой системе не может быть
двух электронов с одинаковой четверкой квантовых чисел
n, l, m, ms. Здесь n = 1,
2, 3, ... - главное квантовое число; l = 0, 1, ..., (n – 1) -
орбитальное квантовое число; m = -l,
..., 0, ..., +l -
магнитное квантовое число; ms =
±1/2
- спиновое квантовое число.
Совокупность электронов, характеризующихся
фиксированными значениями n и l и отличающихся только
значениями m и ms, образуют
электронную оболочку.
Совокупность оболочек с одинаковыми значениями
n образует электронный слой, состоящий из оболочек
с l =
0, 1, ... , (n – 1). Слои электронов обозначают
символами: K (n = 1), L (n = 2), M (n = 3), N (n =
4), O (n = 5), P (n = 6) и т.д. Максимальное число
электронов в слое Nmax =
2n2.
Состояния электронов в оболочке обозначают буквами:
s (l = 0), p (l =
1), d (l = 2), f
(l = 3), g
(l = 4), h
(l = 5).
Число электронов, находящихся на одной
оболочке указывается числовым индексом у буквенного
обозначения состояния, например,
s2.
Вращательная энергия двухатомной молекулы определяется как
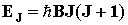 , , 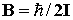
где B – вращательная постоянная, I – момент инерции молекулы, J – вращательное квантовое число (J = 0, 1, 2, ...).
Возможны лишь такие переходы между вращательными энергетическими уровнями, которые подчиняются следующему правилу отбора по магнитному квантовому числу
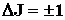 . .
Коротковолновая граница
lmin сплошного
рентгеновского спектра, возбуждаемого при торможении
электронов, определяется как 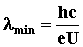 , ,
где e -
заряд электрона, U - разность потенциалов, приложенная
к трубке.
Частота спектральных линий
характеристического рентгеновского излучения определяется
законом Мозли: 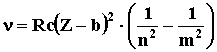 , где R
- , где R
-
постоянная Ридберга, b -
постоянная экранирования, Z - заряд ядра,
n и m - номера уровней. Для
Кa-линии
характеристического рентгеновского излучения b = 1,
n = 1, m = 2. Формула Вульфа-Брэггов:
2dsinq = nl, где q - угол скольжения
рентгеновских лучей, n – порядок отражения,
l - длина волны
рентгеновского излучения, d - межплоскостное
расстояние.
Энергия связи e ядра изотопа
определяется как
e = c2×Dm,
где с - скорость света в вакууме, Dm - разность между массой частиц, составляющих ядро, и
массой самого ядра. 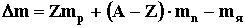 , где Z -
порядковый номер изотопа, А - массовое число,
mp, mn,
mя - массы протона, нейтрона и ядра.
Dm -
дефект массы ядра. Если выразить массу нуклонов в а.е.м. и
учесть, что с2×1 а.е.м. = 931 МэВ, то энергия связи ядра в
мегаэлектронвольтах находится как , где Z -
порядковый номер изотопа, А - массовое число,
mp, mn,
mя - массы протона, нейтрона и ядра.
Dm -
дефект массы ядра. Если выразить массу нуклонов в а.е.м. и
учесть, что с2×1 а.е.м. = 931 МэВ, то энергия связи ядра в
мегаэлектронвольтах находится как
 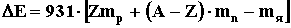 . Энергия связи
eо, приходящаяся на один
нуклон, называется удельной энергией связи ядра . Энергия связи
eо, приходящаяся на один
нуклон, называется удельной энергией связи ядра 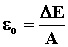 . .
Изменение энергии при ядерной
реакции определяется соотношением
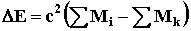 , где aMi - сумма масс частиц, вступивших в ядерную реакцию и
aMk - cумма масс
образующихся частиц. Если aMi > aMk, то реакция идет с
выделением энергии, если aMi
< aMk, то реакция идет с
поглощением энергии. , где aMi - сумма масс частиц, вступивших в ядерную реакцию и
aMk - cумма масс
образующихся частиц. Если aMi > aMk, то реакция идет с
выделением энергии, если aMi
< aMk, то реакция идет с
поглощением энергии.
Количество атомов радиоактивного
вещества dN, распадающихся за
время dt, пропорционально количеству наличных атомов
N и определяется
соотношением 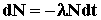 , где
l - постоянная
радиоактивного распада. Интегрируя, получим , где
l - постоянная
радиоактивного распада. Интегрируя, получим 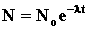 , где
No - первоначальное число атомов, N -
число атомов, не распавшихся к моменту времени t.
Период полураспада T и постоянная распада
l связаны соотношением , где
No - первоначальное число атомов, N -
число атомов, не распавшихся к моменту времени t.
Период полураспада T и постоянная распада
l связаны соотношением
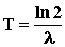 . Величина, обратная
постоянной распада t = 1/l,
представляет среднее время жизни радиоактивного
атома. . Величина, обратная
постоянной распада t = 1/l,
представляет среднее время жизни радиоактивного
атома.
Число атомных распадов,
совершающихся в радиоактивном элементе за одну секунду,
называется активностью этого элемента
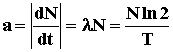 . .
|