|
Избранные лекции
Тепловое излучение
1.1.
РАВНОВЕСНОЕ ТЕПЛОВОЕ СОСТОЯНИЕ.
1
1.2. ХАРАКТЕРИСТИКИ ТЕПЛОВОГО ИЗЛУЧЕНИЯ.
2
1.3. ЗАКОН КИРХГОФА.
5
1.3.1. СЛЕДСТВИЯ ЗАКОНА КИРХГОФА.
5
1.4. ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО ЧЕРНОГО
ТЕЛА.
6
1.5. ФОРМУЛЫ ВИНА И РЭЛЕЯ - ДЖИНСА.
9
1.6. ФОРМУЛА ПЛАНКА.
10
1.7. ПРИМЕНЕНИЕ ЗАКОНОВ ТЕПЛОВОГО
ИЗЛУЧЕНИЯ.
12
1.7.1. ТЕПЛОВЫЕ ИСТОЧНИКИ СВЕТА.
12
1.7.2. ОПТИЧЕСКАЯ ПИРОМЕТРИЯ.
13
1.7.3. НОЧНОЕ ВИДЕНИЕ.
16
ЛИТЕРАТУРА.
17
Рассмотренные ранее в курсе общей физики
явления интерференции, дифракции, дисперсии и поляризации
света с несомненностью показали, что свет обладает волновыми
свойствами. Однако последующее изучение взаимодействия света с
веществом выявило, что свету, помимо указанных волновых
свойств, присущи еще и другие (корпускулярные), которые
мы привыкли считать атрибутами частиц – тел, локализованных в
определенном объеме, обладающих определенной массой
m, импульсом p
и соответствующей кинетической энергией. В связи с этим
возникло новое представление, рассматривающее световой поток
как поток своеобразных частиц – квантов света (фотонов).
Впервые недостаточность волновых
представлений о свете проявилась при изучении законов
теплового излучения абсолютно черных тел.
Тепловое излучение – это
электромагнитное излучение, испускаемое веществом и
возникающее за счет энергии теплового движения атомов и
молекул (т.е. внутренней энергии).
Тепловое излучение (ТИ) свойственно всем
телам при температурах выше абсолютного нуля. ТИ можно
поддерживать неизменным, подводя непрерывно к телу
соответственное количество тепла. Т.е. тепловое излучение
может быть равновесным, нетепловое – обязательно неравновесно.
Если несколько нагретых (теплоизлучающих) тел окружить
идеально отражающей, непроницаемой для излучения оболочкой, то
по истечении некоторого интервала времени в системе
«излучающие тела + излучение в полости» установится
термодинамическое равновесие (рис.1). Следовательно,
температуры тел выровняются, а распределение энергии между
телами и излучением не будет меняться со временем. Такое
равновесное состояние системы устойчиво, т.е. после всякого
нарушения его, состояние равновесия восстанавливается.
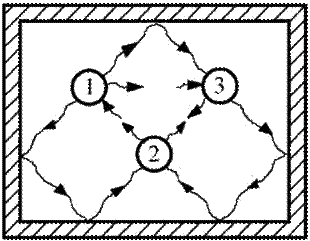
Рис. 1.
Причем, термодинамическое равновесие
устанавливается в полости, стенки которой выполнены из любого
реального материала и поддерживаются при некоторой неизменной
температуре.
Всякое другое излучение, возбуждаемое не
нагреванием, а каким-либо иным способом, не приводит к
установлению термодинамического равновесия. Например, если
внутрь упомянутой выше полости поместить тело, светящееся
благодаря предварительному облучению ультрафиолетовыми лучами,
то свечение этого тела постепенно ослабнет и прекратится. Это
произойдет потому, что поглощаемые телом лучи (находящиеся в
полости благодаря отражению стенками оболочки) не способны
вновь вызвать свечение тела. Таким образом, способность ТИ
находиться в равновесии с излучающим телом отличает ТИ от
других видов излучения тел, поскольку нетепловое излучение
всегда неравновесно.
1.2. ХАРАКТЕРИСТИКИ ТЕПЛОВОГО
ИЗЛУЧЕНИЯ
Основной величиной, характеризующей
тепловое состояние тел, является температура. Для спектральной
характеристики теплового излучения вводится понятие об
излучательной ( или лучеиспускательной) способности тела (ее
часто также называют спектральной плотностью энергетической
светимости тела) rλ,T,
которая равна
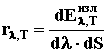 (1), (1),
где 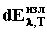 – энергия электромагнитного излучения,
испускаемого за единицу времени с элемента поверхности
dS тела в пределах спектрального
интервала длин волн от λ до λ+dλ. – энергия электромагнитного излучения,
испускаемого за единицу времени с элемента поверхности
dS тела в пределах спектрального
интервала длин волн от λ до λ+dλ.
Таким образом, излучательная
способность тела численно равна мощности излучения
с единицы площади поверхности этого тела в единичном интервале
длин волн.
Излучательная способность зависит как от
длины волны λ, вблизи которой взят интервал
dλ, так и от температуры тела
T. Из (1) видно, что в системе
единиц СИ rλ
измеряется в Дж/с·м3.
Интегральной характеристикой излучения
является светимость (иначе энергетическая светимость или
интегральная излучательная способность)тел.
Светимость R(T)
– количество энергии, излучаемое единицей поверхности тела в
единицу времени во всем интервале длин волн от 0 до ∞.
Таким образом:
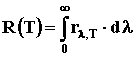 (2). (2).
Все тела в той или иной степени поглощают
энергию падающих на них электромагнитных волн. Спектральной
характеристикой поглощения является поглощательная
способность тела (или коэффициент монохроматического
поглощения):
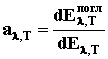 (3), (3),
показывающая, какая доля энергии
dEλ,T,
доставляемой за единицу времени на единицу площади поверхности
тела падающими на нее электромагнитными волнами спектрального
интервала dλ, поглощается
телом. Т.е. 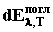 – количество энергии спектрального
интервала dλ, поглощаемой
площадкой тела dS в единицу
времени, а dEλ,T
– количество энергии того же спектрального интервала,
падающего в единицу времени на эту площадку. Очевидно, что
aλ,T
– величина безразмерная. – количество энергии спектрального
интервала dλ, поглощаемой
площадкой тела dS в единицу
времени, а dEλ,T
– количество энергии того же спектрального интервала,
падающего в единицу времени на эту площадку. Очевидно, что
aλ,T
– величина безразмерная.
Величины aλ,T
и rλ,T
являются функциями длины волны и температуры:
aλ,T
= f(λ,
T),
rλ,T
= f(λ,
T). При изменении температуры
тела меняются как его излучательная способность, так и
поглощательная.
Зависимость поглощательной способности
различных тел от длины волны при данной температуре приведены
на рис.2.

Рис. 2.
При изменении температуры произвольного
тела («белого» тела) характер кривой
aλ,T
= f (λ,
T)
может измениться: лучи, сильно поглощающиеся при одной
температуре, могут пропускаться при другой температуре и
наоборот (рис.2в).
Тело, которое поглощает полностью все
падающее на него излучение любой длины волны при любой
температуре, называют абсолютно черным (точнее
абсолютно поглощающим) телом. Его поглощательная
способность для всех длин волн при любых температурах равна
единице (рис.2а). Абсолютно черных тел (АЧТ) в природе нет.
Тела, называемые черными, поглощают хорошо только излучение
видимой области спектра, да и это излучение поглощают не
полностью. Так, например, черная бумага, в которую
заворачивают фотопластинки, поглощает только 95% падающего
света. Сажа, лучше всего поглощающая лучи видимого света
(98%), хуже поглощает инфракрасное (ИК) излучение.
Хорошей моделью абсолютно черного тела
является полое тело с небольшим по сравнению с размерами тела
отверстием на поверхности (рис.3).

Рис. 3.
Луч, попавший внутрь такой полости, может
выйти из нее только после многократных отражений. При каждом
отражении от стенок полости часть энергии луча поглощается и
лишь ничтожная доля энергии лучей, попавших в отверстие,
сможет выйти обратно. Следовательно, поглощательная
способность отверстия весьма близка к 1. Полость с малым
отверстием представляет собой практически абсолютно черное
тело.
Отметим, что если стенки полости
поддерживать при некоторой температуре T,
то отверстие будет излучать, и это излучение с большой
степенью точности можно считать излучением абсолютно черного
тела, имеющего температуру T.
Встречаются тела, называемые «серыми», для
которых поглощательная способность одинакова для всех частот и
зависит только от температуры (материала и состояния
поверхности). Для них зависимость поглощательной способности
от λ при данной температуре выражается прямой, ордината
которой меньше единицы (рис.2б).
1.3. ЗАКОН КИРХГОФА[1]
Установлено, что излучательные и
поглощательные способности тел пропорциональны друг другу
(например, сажа или платиновая чернь имеют большие значения
aλ,T
и rλ,T;
а полированное серебро обладает малыми aλ,T
и rλ,T).
Получение света от пламени горящей свечи основано на этой
пропорциональности между aλ,T
и rλ,T.
В пламени имеются частицы сажи, обладающие большим
поглощением, они и дают яркий свет. Если пламя не содержит
частиц сажи (пламя газовой горелки), оно не будет светиться.
Результаты экспериментальных исследований и
термодинамические рассуждения позволили Кирхгофу показать, что
действительно между излучательной и поглощательной
способностью различных тел существует связь, и что отношение
излучательной способности тела к его поглощательной
способности является одинаковым для всех тел:
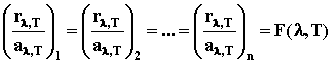 (4), (4),
индексы 1, 2,… n
относятся к 1-му, 2-му и т.д. телам.
Таким образом,
для всех тел, независимо от их природы, отношение
излучательной способности к поглощательной способности при той
же температуре и для тех же длин волн есть универсальная
функция от длины волны и температуры (универсальная функция
Кирхгофа).
1.3.1. СЛЕДСТВИЯ ЗАКОНА
КИРХГОФА
Допустим, что одно из тел – абсолютно
черное тело. Обозначим его излучательную способность
uλ,T.
Учитывая, что поглощательная способность АЧТ равна 1, можем
записать закон Кирхгофа так:
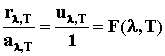 (5).
(5).
Следовательно, универсальная функция
Кирхгофа F(λ,T)
есть излучательная способность АЧТ, т.е.
F(λ,
T) = uλ,
T
(6),
поэтому отношение излучательной способности
к поглощательной способности произвольного тела равно
излучательной способности АЧТ для той же длины волны и при той
же температуре.
Из (5) следует, что rλ,T
= aλ,T
· uλ,T,
а так как aλ,T
< 1, то rλ,T
< uλ,T.
Следовательно, тепловое излучение любого тела в любой области
спектра всегда меньше, чем излучение АЧТ в этой же области
спектра и при этой же температуре.
Проиллюстрируем вышесказанное с помощью
экспериментальных кривых распределения энергии в спектре
излучения АЧТ (1), «серого» тела (2) и произвольного тела (3),
т.е. зависимостей rλ,T(λ)
при T =
const (рис. 4).
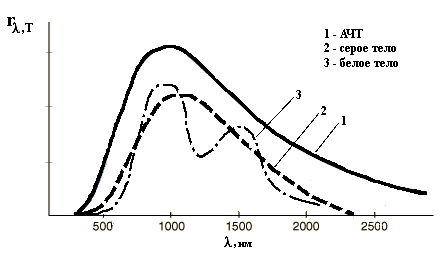
Рис. 4.
Кривая для серого тела может быть получена
из кривой uλ,T
для АЧТ путем умножения ординат последней на постоянный
множитель, меньший 1 и равный поглощательной способности
серого тела. Излучение других тел является селективным
(избирательным). Кривая rλ,T(λ)
таких тел может иметь несколько максимумов и минимумов, но вся
она лежит ниже uλ,T
АЧТ, как и следует из закона Кирхгофа.
Таким образом, зная излучательную
способность и светимость (интегральную излучательную
способность) АЧТ, можно вычислить их для любого нечерного
тела, если известна поглощательная способность последнего,
которая должна быть определена экспериментально.
1.4. ЗАКОНЫ ИЗЛУЧЕНИЯ АБСОЛЮТНО
ЧЕРНОГО ТЕЛА
После установления закона Кирхгофа стало
очевидным, что первоочередная задача теории теплового
излучения состоит в нахождении функции Кирхгофа, т.е. в
выяснении вида зависимости излучательной способности
uλ,T
АЧТ от его температуры и длины волны. Поскольку излучательная
способность АЧТ является универсальной функцией λ и
Т, то спектральный состав и энергия излучения АЧТ не
зависит от природы тела.
Сначала удалось решить более простую задачу
– найти зависимость интегральной излучательной способности (R)
АЧТ от его температуры.
В 1884г. Л.Больцман,
применив к исследованию равновесного теплового излучения
термодинамический метод, теоретически показал, что внутри
замкнутой полости интегральная излучательная способность АЧТ
пропорциональна четвертой степени его абсолютной температуры:
R =
σ · T4
. (7)
Коэффициент пропорциональности σ
называется постоянной Стефана-Больцмана. В результате
многочисленных экспериментов найдено, что σ = 5,67 · 10-8
Вт·м-2
×К-4.
Этот закон получил название закона
Стефана-Больцмана, т.к. еще в 1879г. И.Стефан
на основе анализа экспериментальных данных пришел к
аналогичному выводу. Однако он ошибочно считал, что светимость
любого тела также пропорциональна 4-ой степени его абсолютной
температуры.
Закон Стефана-Больцмана указывает на
чрезвычайно быстрый рост мощности излучения АЧТ с возрастанием
температуры.
Например, при повышении температуры с 800 до 2400К (т.е. с 527
до 2127 оС) излучение АЧТ возрастает в 81 раз.
К другим (не АЧТ) телам закон
Стефана-Больцмана не может быть применен, так как эксперименты
показывают, что для таких тел с изменением температуры
изменяется как коэффициент σ, так и показатель степени
при Т.
Значительно более сложной оказалась задача
отыскания вида функции Кирхгофа F(λ,T),
т.е. выяснение спектрального состава излучения АЧТ. Решение
этой задачи вышло далеко за рамки теории теплового излучения и
сыграло огромную роль во всем дальнейшем развитии физики, так
как привело к установлению квантового характера излучения и
поглощения энергии атомами и молекулами.
Эксперименты (с помощью моделей АЧТ)
показали, что зависимость излучательной способности АЧТ
uλ,T
от длины волны при разных температурах АЧТ имеет вид,
показанный на рис.5.
Как следует из рис.5:
1.
Спектр излучения АЧТ имеет
сплошной характер, т.е. в спектре этого излучения представлен
непрерывный ряд длин волн.
2.
Существует отчетливо выраженный
максимум излучательной способности, который с повышением
температуры смещается в сторону более коротких волн.
3.
Излучательная способность АЧТ
уменьшается в сторону коротких волн значительно более резко,
чем в сторону длинных волн.
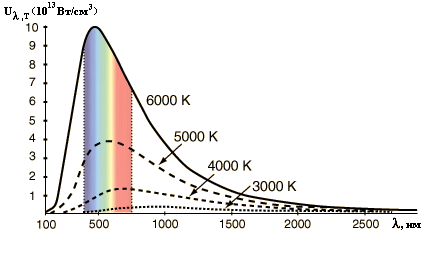 а) а)
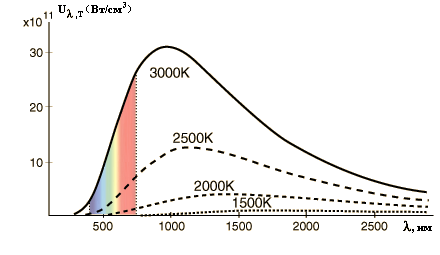 б) б)
Рис. 5.
Тщательное количественное исследование
кривых, приведенных на рис.5, позволило установить следующие
соотношения:
1.
R =
σ · T4
– Стефан, из экспериментальных кривых.
2.
Длина волны λm,
на которую приходится максимум излучательной способности АЧТ,
обратно пропорциональна абсолютной температуре тела:
λm
= b1 /
T или λm
· T = b1
(8),
это соотношение (8) носит название закона
смещения Вина. Постоянная b1,
называемая постоянной Вина равна 2,898.10-3
м.К.
3.
Максимальное значение излучательной
способности АЧТ возрастает прямо пропорционально 5-ой степени
абсолютной температуры:
(uλ,T)max
= b2 ·
T5, где b2
= 1,3·10-5 вт·м-3·К-5.
Таким образом, при повышении температуры
растет не только полное излучение АЧТ, но и изменяется
распределение энергии по спектру. Например, при малых
температурах тела излучаются главным образом ИК лучи, а по
мере повышения температуры излучение делается красноватым,
оранжевым и затем белым (смещается в сторону коротких волн).
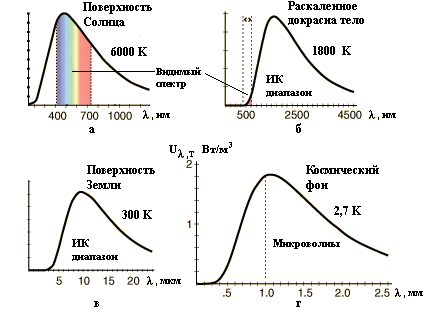
Рис. 6.
Закон Стефана-Больцмана позволяет
определить интегральную излучательную способность АЧТ по его
температуре. Закон смещения Вина связывает температуру тела с
длиной волны, на которую падает максимальная излучательная
способность. Но ни тот, ни другой законы не решают основной
задачи о том, как велика излучательная способность,
приходящаяся на каждую длину волны в спектре АЧТ при
температуре Т. Для этого надо установить функциональную
зависимость uλ,Т
от λ и Т.
1.5. ФОРМУЛЫ ВИНА И
РЭЛЕЯ-ДЖИНСА
Основываясь на непрерывном характере
испускания электромагнитных волн и на законе равновесного
распределения энергии по степеням свободы, были теоретически
получены две формулы для излучательной способности АЧТ:
1.
Формула Вина: Uλ,T = a1 ·
λ-3
· exp(-a2/λT)
(9),
где a1,
a2 – постоянные
величины.
2. Формула Рэлея-Джинса:
Uλ,T
= a3 · λ-3 ·
k · T
(10),
где k –
постоянная Больцмана.
Опытная проверка показала, что для данной
температуры формула Вина верна для коротких волн, когда
λ·T→0
и дает резкие расхождения с опытом в области длинных волн.
Формула Рэлея-Джинса оказалась верна для длинных волн и
совершенно не применима для коротких (рис.7)
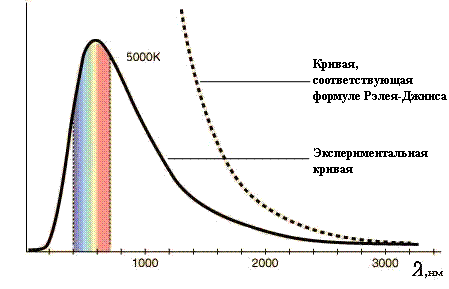
Рис. 7.
Так как формула Рэлея-Джинса, опирающаяся
на классическую физику, в резком противоречии с опытом,
приводит к заключению, что в спектре теплового излучения
большая часть энергии приходится на фиолетовую часть спектра,
то это положение было названо Эренфестом «Ультрафиолетовой
катастрофой».
Подводя итог сказанному, видим, что
классическая физика в теории теплового излучения потерпела
решительное поражение. По образному выражению Лоренца,
«уравнения классической физики оказались неспособными
объяснить, почему угасшая печь не испускает желтых лучей
наряду с излучением больших длин волн».
Таким образом, к концу 19 столетия
существовали две формулы, полученные теоретически, каждая из
которых соответствовала экспериментальным данным в
ограниченном участке спектра, но ни одна из них не описывала
всю экспериментальную кривую.
1.6. ФОРМУЛА ПЛАНКА
В конце 1900г. Планку удалось найти сначала
чисто эмпирически формулу для излучательной способности АЧТ,
которая хорошо согласовывалась с данными опыта и в двух
предельных случаях (для длинных и коротких волн) переходила
соответственно в формулу Рэлея-Джинса, либо в формулу Вина.
Основной же этап исследований, завершенный
Планком в декабре 1900г., состоял в выяснении физического
смысла и теоретического обоснования столь удачно угаданного им
соотношения. Применив статистический метод Больцмана, Планк
вывел искомые соотношения. Однако для этого ему пришлось
ввести так называемую квантовую гипотезу,
заключающуюся в том, что поглощение и испускание энергии
электромагнитного излучения атомами и молекулами возможно
только отдельными «порциями», которые получили название
квантов энергии.
Величина кванта энергии ε
пропорциональна частоте излучения
n
(обратно пропорциональна длине волны λ
:
ε = h·ν
= h·c/λ
(11).
Коэффициент пропорциональности
h = 6,626176·10-34
Дж·с называется постоянной Планка. Именно крайне малая
величина h является причиной
того, что дискретность, требуемая законами атомной физики,
совершенно не сказывается при изучении макроскопических
явлений.
Окончательное выражение, полученное Планком
для излучательной способности АЧТ, имеет вид:
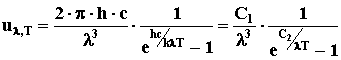 (12), (12),
где C1
= 2πhc, C2
= hc/k,
где c – скорость света в
вакууме; k – постоянная
Больцмана.
Кривая, соответствующая формуле (12)
совпадает с экспериментальной кривой uλ,T
(рис.7). Зная величину постоянной Планка
h и частоту или длину волны
света, мы можем вычислить величину кванта энергии для любого
участка спектра АЧТ.
Из формулы Планка (12) как частный случай
получаются закон Стефана-Больцмана и закон Вина. Действительно
для светимости АЧТ получаем:
 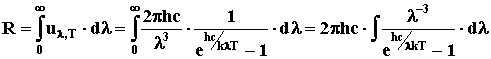
Вводя новую переменную x
= hc/(λkT),
преобразуем выражение:
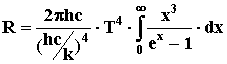
Обозначив произведение всех постоянных
множителей через σ, получим формулу
R = σ·T4,
соответствующую закону Стефана-Больцмана. Расчет σ по
этой формуле дает результат, совпадающий с эмпирическим
значением постоянной Стефана-Больцмана.
Закон смещения Вина и его константу можно
получить из формулы Планка нахождением максимума функции
uλ,T,
для чего берется производная от uλ,T
по λ и приравнивается 0. Вычисление приводит к формуле:
 . .
Расчет постоянной b1
по этой формуле дает результат, совпадающий с эмпирическим
значением постоянной Вина.
1.7. ПРИМЕНЕНИЯ ЗАКОНОВ
ТЕПЛОВОГО ИЗЛУЧЕНИЯ
1.7.1. ТЕПЛОВЫЕ ИСТОЧНИКИ СВЕТА
Большинство искусственных источников света
является тепловыми излучателями (электрические лампы
накаливания, обычные дуговые лампы и т.п.). Однако эти
источники света не являются экономичными.
Как известно, глаз человека обладает
чувствительностью только к очень узкому участку спектра (от
0,380 мкм до 0,770 мкм). Все остальные волны не вызывают
зрительного ощущения. Максимальная чувствительность глаза
соответствует λ = 0,555 мкм.
Исходя из этого свойства глаза, следует
требовать от источников света такого распределения энергии в
спектре, при котором максимальная излучательная способность
попадала бы на λ = 0,555 мкм или около нее.
Если в качестве такого источника взять АЧТ,
то п о закону смещения Вина можно вычислить его абсолютную
температуру . Таким образом, наиболее выгодный тепловой
источник света должен иметь температуру примерно 5200К, что
хорошо соответствует температуре солнечной поверхности. Такое
совпадение является результатом биологического приспособления
человеческого зрения к распределению энергии в спектре
солнечного излучения. Но и у этого источника света КПД
(отношение энергии видимого излучения к энергии всего
излучения) будет невелик (рис.6а). Расчет показывает, что при
T = 5000-6000К, КПД ~14-15%. о закону смещения Вина можно вычислить его абсолютную
температуру . Таким образом, наиболее выгодный тепловой
источник света должен иметь температуру примерно 5200К, что
хорошо соответствует температуре солнечной поверхности. Такое
совпадение является результатом биологического приспособления
человеческого зрения к распределению энергии в спектре
солнечного излучения. Но и у этого источника света КПД
(отношение энергии видимого излучения к энергии всего
излучения) будет невелик (рис.6а). Расчет показывает, что при
T = 5000-6000К, КПД ~14-15%.
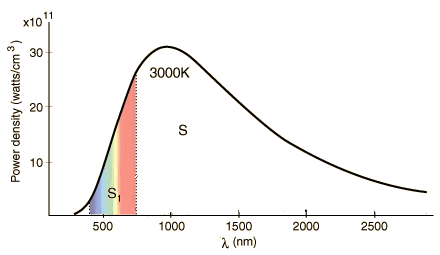
Рис. 8.
При температуре же существующих
искусственных источников света примерно 3000К, КПД
h~1-3%,
что видно из соотношения площадей S1
и S (рис.8), где
S1 выражает энергию
излучения видимой области спектра, S
– всю энергию излучения.
Такая невысокая «световая отдача» теплового
излучателя объясняется тем, что при хаотичном движении атомов
и молекул возбуждаются не только световые (видимые), но и
другие электромагнитные волны, которые не оказывают светового
воздействия на глаз.
Важнейшие из современных температурных
источников света – электрические лампы накаливания с
вольфрамовой нитью (температура плавления Тпл.=3655К).
Однако, нагрев нити до Т>2500К опасен, т.к. вольфрам
быстро распыляется и нить разрушается. Для уменьшения
распыления нити было предложено наполнять лампы инертным газом
(Ar, Xe,
N) при давлении
p~0,5 атм. Это позволило поднять
Т нити до 3000-3200К. При этих температурах максимум
излучательной способности лежит в области ИК волн (~1,1 мк),
поэтому все современные лампы накаливания имеют
η~1%.
1.7.2. ОПТИЧЕСКАЯ ПИРОМЕТРИЯ
Изложенные выше законы излучения АЧТ
позволяют определить температуру этого тела, если известна
длина волны λm,
соответствующая максимуму uλ,T
(закон Вина) или если известна величина светимости (закон
Стефана-Больцмана). Методы определения температуры тела по
его тепловому излучению называются оптической пирометрией
(ОП). Они особенно удобны при измерении высоких
температур. В зависимости от метода наблюдения оптически
определяется одна из трех условных температур: радиационная,
цветовая и яркостная. Переход к истинной температуре требует
знания дополнительных параметров излучающего тела.
Приборы для измерения температуры
непрозрачных тел по их излучению в оптическом диапазоне
спектра называются пирометрами (от греч. pýr — огонь).
Тело, температуру которого определяют при
помощи пирометра, должно находиться в тепловом равновесии и
обладать коэффициентом поглощения, близким к единице.
Поскольку упомянутые законы применимы к АЧТ,
то ОП, основанная на них, дает хорошие результаты только при
измерении температур тел, близких по своим свойствам к АЧТ
(заводские печи, лабораторные муфельные печи, топки котлов и
т.п.).
Способы определения
температуры тепловых излучателей
а) Метод, основанный на законе смещения
Вина
Если нам известна та длина волны
λ =
λm,
на которую приходится максимум излучательной способности, то
температура тела легко определяется (λmТ
= b1).
В частности, так определяется температура на поверхности
Солнца, звезд и т.д.
б) Радиационный способ измерения Т
В основе этого способа лежит измерение
светимости тела R. Соответствующие
приборы называются радиационными пирометрами (РП).
Естественно, что если излучающее тело не
является АЧТ, то РП не даст истинной температуры тела, а
покажет ту температуру АЧТ, при которой интегральная
излучательная способность последнего RАЧТ
= Rиспыт.тела. Такая
температура тела называется радиационной или энергетической
температурой.
Из недостатков РП укажем на невозможность
его применения для определения температур небольших объектов,
а также на влияние среды, находящейся между объектом и
пирометром, которая поглощает часть излучения.
в) Яркостный метод определения температур
Данный метод основан на визуальном
сравнении яркости свечения раскаленной нити лампы пирометра с
яркостью изображения накаленного испытуемого тела (рис. 9).
Виды пирометров
Основным типом является яркостный
пирометр, обеспечивающий наибольшую точность измерений
температуры в диапазоне 103—104
К. В простейшем визуальном яркостном пирометре с исчезающей
нитью (рис. 9) объектив фокусирует изображение исследуемого
тела на плоскость, в которой расположена нить (ленточка)
эталонной лампы накаливания. Через окуляр и красный фильтр,
позволяющий выделять узкую спектральную область около длины
волны λ
= 0,65 мкм, нить
рассматривают на фоне изображения тела и, изменяя ток накала
нити, добиваются выравнивания яркостей нити и тела (нить в
этот момент становится неразличимой).


Рис. 9.
Шкала прибора, регистрирующего ток накала,
прокалибрована обычно в °С или К, и в момент выравнивания
яркостей прибор показывает так называемую яркостную
температуру (Tb) тела. Истинная температура
тела Т определяется на основе законов теплового
излучения Кирхгофа и Планка по формуле:
Т = Tbc2/(c2
+λэּ Тb
ּ
ln
aλ,T)
(13),
где c2
= 0,014388 м ּК,
aλ,T
— коэффициент поглощения тела,λэ
— эффективная длина волны пирометра.
Точность результата в первую очередь
зависит от строгости выполнения условий измерений (aλ,T
≈
1 и др.). Основная инструментальная погрешность обусловлена
нестабильностью температурной лампы. Заметную погрешность
могут вносить также индивидуальные особенности глаза
наблюдателя. У фотоэлектрических пирометров
(рис. 10) этот вид погрешности отсутствует. Погрешность
образцовых лабораторных фотоэлектрических пирометров не
превышает сотых долей градуса при Т=1273 К.
Промышленные серийные фотоэлектрические пирометры обладают на
порядок большей погрешностью, визуальные — ещё на порядок
большей.


Рис. 10.
Для измерения температуры тел, у которых
a ≈ const в оптическом диапазоне
спектра, применяют цветовые пирометры. Этими
пирометрами определяют обычно отношение яркостей в синей и
красной областях спектра b1(λ1,
T)/b2(λ2,
T) (например, для длин волн
λ1
= 0,48 мкм и
λ2
= 0,60 мкм). Шкала
прибора прокалибрована в °С и показывает цветовую температуру
Tc. Истинная температура Т тела
определяется по формуле
 (14). (14).
Цветовые пирометры менее точны, менее
чувствительны и более сложны, чем яркостные и применяются в
том же диапазоне температур.
Наиболее чувствительны (но и наименее
точны) радиационные пирометры, или пирометры
суммарного излучения, регистрирующие полное излучение тела.
Действие их основано на законах излучения
Стефана-Больцмана и
Кирхгофа. Объектив радиационных пирометров
фокусирует наблюдаемое излучение на приёмник (обычно
термостолбик или болометр), сигнал которого регистрируется
прибором, прокалиброванным по излучению абсолютно чёрного тела
и показывающим
радиационную температуру Tr.
Истинная температура определяется по формуле
 (15),
(15),
где aT
— полный коэффициент поглощения тела. Радиационными
пирометрами можно измерять температуру, начиная с 200°С. В
промышленности пирометры широко применяют в системах контроля
и управления температурными режимами разнообразных
технологических процессов.
1.7.3. НОЧНОЕ ВИДЕНИЕ
Ночью при отсутствии солнечного света
человек в темноте перестает видеть окружающие его предметы.
Однако, все они, имея ненулевую температуру, испускают
электромагнитное тепловое излучение и ночью. С помощью закона
Вина можно оценить длину волны, на которую приходится максимум
излучательной способности тела, если известна его температура.
Из этой оценки следует, что при средней температуре тел
порядка 300 К основная энергия их теплового излучения
приходится на инфракрасное излучение с длиной волны порядка 10
мкм (рис.6в). Излучение в видимой области спектра (0,4 мкм
< λ
< 0,7 мкм) при таких
температурах имеет слишком малую энергию и не может быть
обнаружено невооруженным глазом.
Так как в сторону неба система наземных тел
не является замкнутой, то равновесия между телами у
поверхности Земли и их излучением не устанавливается. А значит
все тела, температура которых несколько больше, чем
температура земной поверхности, могут быть зафиксированы в
микроволновом диапазоне как излучающие объекты. Увидеть такие
источники инфракрасного излучения можно только с помощью
специальных приборов, в которых микроволновое невидимое глазом
излучение регистрируется специальными датчиками инфракрасного
излучения и преобразуется в модулированные электрические
сигналы, которые управляют электронным пучком, дающим на
экране кинескопа видимое изображение предметов.
В конце XX века произошло качественное
изменение техники ночного видения, связанное с созданием
электронно-оптических преобразователей нового типа. С помощью
современных биноклей и прицелов ночного видения наблюдатель
может получить в темноте видимое изображение достаточно
высокого качества человека на расстоянии нескольких сот метров
или движущегося танка на расстоянии нескольких километров. А
пилотажные очки ночного видения позволяют эксплуатировать
вертолеты в условиях ограниченной видимости практически
круглые сутки.
Литература
1.
Геворкян Р.Г., Шепель В.В. Курс
общей физики. 2-е изд., перераб. – М.: «Высшая школа», 1966.
С.465-478.
2.
Грабовский Р.И. Курс физики. 8-е
изд., стер. – СПб.: Издательство «Лань», 2005. с.498-506.
3.
Детлаф А.А., Яворский Б.М. Курс
физики: Учеб. пособие для вузов. – М.: «Высшая школа», 1989.
с.400-409.
4.
Савельев И.В. Курс общей физики:
Учеб. пособие. В 3-х т. Т. 3. Квантовая оптика. Атомная
физика. Физика твердого тела. Физика атомного ядра и
элементарных частиц. – 3-е изд., испр. – М.: «Наука», 1987.
с.9-31.
5.
Сивухин Д.В. Общий курс физики:
оптика. – М.: «Наука», 1980. с.675-704.
6.
Трофимова Т.И. Курс физики. 7-е
изд., стер. – М.: «Высшая школа», 2003. с.367-376.
Кирхгоф (Kirchhof)
Густав Роберт (1824 – 1887 гг.) – немецкий физик,
иностранный член-корреспондент Петербургской АН (1862).
Установил правила для электрической цепи, названные его
именем. Совместно с Р.Бунзеном, заложил основы
спектрального анализа (1859), открыл цезий (1860) и
рубидий (1861). Ввел понятие абсолютно черного тела и
открыл закон излучения, названный его именем.
Больцман (Boltzmann)
Людвиг (1844 – 1906 гг.) австрийский физик, один из
основателей статистической физики, иностранный член
корреспондент Петербургской АН (1899). Вывел функцию
распределения, названную его именем, и основное
кинетическое уравнение газов. Дал (1872) статистическое
обоснование II начала
термодинамики. Вывел закон излучения.
Стефан (Stefan)
Иозеф (1835 – 1893 гг.) австрийский физик.
Экспериментально установил (1879) закон излучения АЧТ
(закон Стефана-Больцмана). Труды по диффузии и
теплопроводности газов, оптике и др.
|