|
Решения и указания к
решениям
2. КОРПУСКУЛЯРНЫЕ СВОЙСТВА ЭЛЕКТРОМАГНИТНОГО
ИЗЛУЧЕНИЯ
3. МОДЕЛЬ АТОМА РЕЗЕРФОРДА -
БОРА
4. ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ. СООТНОШЕНИЕ
НЕОПРЕДЕЛЕННОСТЕЙ ГЕЙЗЕНБЕРГ
5. ЭЛЕМЕНТЫ
КВАНТОВОЙ МЕХАНИКИ
6. ЭЛЕКТРОННАЯ ОБОЛОЧКА АТОМА. МОЛЕКУЛЯРНЫЕ
СПЕКТРЫ
7. РЕНТГЕНОВСКОЕ
ИЗЛУЧЕНИЕ
8. СТРОЕНИЕ АТОМНОГО ЯДРА. ДЕФЕКТ
МАССЫ
9. ЕСТЕСТВЕННАЯ
РАДИОАКТИВНОСТЬ
10. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
1.
ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
1.1. Указание: Мощность излучения
P некоторой поверхностью при условии,
что она является АЧТ, определяется произведением
светимости R
на площадь поверхности S: P
= RS. Светимость АЧТ определяется из
закона Стефана-Больцмана: R
= sT4.
1.6. Указание: поскольку тепло теряется
только вследствие излучения, то необходимо подводить мощность,
равную излучаемой, чтобы тело оставалось нагретым до
определенной температуры.
1.8. Указание: в) Поскольку масса теряется
за счет излучения, то мощность излучения равна:
P
= Dm×c2, а значит: Dm = P
/ c2 = 4.3×109 кг/с; г) Т.к.
температура Солнца остается постоянной, то мощность излучения
DP солнечной поверхности в течение
промежутка времени Dt равна с одной стороны:
DP = Dm1×c2, где Dm1 - уменьшение массы Солнца за время
Dt, а с другой стороны: DP = P×Dt. Тогда, поскольку согласно условию
задачи: Dm1/m º h = 1%, то Dt = hm×c2/DP = 4.5×1018с = 1.43×1011 лет.
1.10.
Металлический шар с
теплоемкостью С и температурой Т выброшен в
межпланетное пространство. Со временем его температура должна
уменьшаться: шар остывает вследствие лучеиспускания. Изменение
внутренней энергии шара при остывании
dE
= dQ
= - C×dT,
где dT
– изменение температуры шара. С другой стороны изменение
внутренней энергии равно:
dE
= R×S×dt
= asT4×S×dt,
а значит:
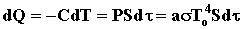 . Разделяем переменные и получаем: . Разделяем переменные и получаем:
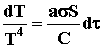 , интегрируя имеем: , интегрируя имеем:
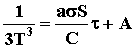 , где А - постоянная интегрирования.
Постоянную А находим из начальных условий: в начальный
момент времени (t
= 0): Т = То, т.е., , где А - постоянная интегрирования.
Постоянную А находим из начальных условий: в начальный
момент времени (t
= 0): Т = То, т.е.,
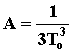 . Отсюда находим закон убывания
температуры Т шара со временем (t): . Отсюда находим закон убывания
температуры Т шара со временем (t):
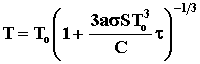 , ,
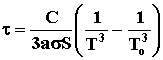 , площадь поверхности шара:
S
= 4pR2.
Из полученных результатов получаем закон изменения времени
остывания с температурой: , площадь поверхности шара:
S
= 4pR2.
Из полученных результатов получаем закон изменения времени
остывания с температурой:
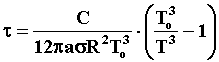 , отсюда получаем время, в течение
которого температура шара уменьшится вдвое: , отсюда получаем время, в течение
которого температура шара уменьшится вдвое:
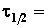 11 мин. 11 мин.
1.11.
Поскольку нити
соединены последовательно, то силы токов
I1
и I2,
протекающих через обе вольфрамовые нити, равны между собой
I1
=
I2
º
I.
Сопротивление нити
r
при неизменной температуре
r
=
rl/S,
где
r - удельное
сопротивление вольфрама,
l - длина нити,
S
=
pd2/4
– площадь
поперечного сечения,
d
– диаметр нити. Мощности Р1 и Р2,
выделяемые в нитях при протекании электрического тока
I:
Р1 =
I2×r1=
4I2×rl1/pd12
и Р2 =
I2×r2=
4I2×rl2/pd22.
За счет подводимой мощности нити накаляются, мощность
излучения может быть получена, исходя из закона
Стефана-Больцмана для серых тел: P1= a1×sT1
4S1,
где S1=
pd1×l1
– площадь поверхности 1-ой нити, а P2= a2×sT2
4S2,
где S2=
pd2×l2
– площадь поверхности 2-ой нити, тогда имеем 4I2×rl1/pd12=
a1×sT14
×pd1×l1
(1), а 4I2×rl2/pd22
= a2×sT24×
pd2×l2
(2). Разделив (1) на (2) имеем:
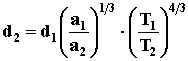 = 0.05 мм. = 0.05 мм.
1.12.
Мощность излучения в интервале
длин волн
Dl:
РDl
= а×ul,T×Dl×S,
где ul,T
– излучательная
способность АЧТ,
S
– площадь поверхности тела, а – коэффициент серости. Согласно
формуле Планка имеем
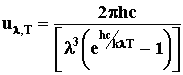 . Длина волны
l
по условию задачи есть длина волны
lm
, соответствующая
максимуму излучения, следовательно:
l
=
lm
– С1/Т (С1
– 1-я постоянная Вина) и
Dl=0.02lm.
Используя полученные уравнения, имеем: . Длина волны
l
по условию задачи есть длина волны
lm
, соответствующая
максимуму излучения, следовательно:
l
=
lm
– С1/Т (С1
– 1-я постоянная Вина) и
Dl=0.02lm.
Используя полученные уравнения, имеем:
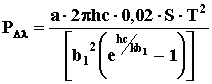 = 0.0435 Вт. = 0.0435 Вт.
2.
КОРПУСКУЛЯРНЫЕ СВОЙСТВА ЭЛЕКТРОМАГНИТНОГО
ИЗЛУЧЕНИЯ
2.4.
При облучении шарика квантами
достаточной энергии возникает внешний фотоэффект. Шарик при
этом заряжается положительно. Покинуть шарик могут электроны с
энергией, достаточной для преодоления потенциального барьера,
т.е. mV2max/2
= eU,
отсюда eU = hn
- A. Таким образом,
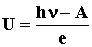 . Подставляя числовые данные задачи, получим
U = 2.26 В. . Подставляя числовые данные задачи, получим
U = 2.26 В.
2.10. Зеркальце приобретает кинетическую
энергию за счёт действия на зеркальце силы светового давления.
Из рисунка 1 для начального состояния (I)
имеем: Еп = 0; Ек
= Е, где Е - энергия лазерного излучения,
Еп и Ек -потенциальная и
кинетическая энергии зеркальца соответственно. Для состояния,
соответствующего наибольшему отклонению (II): Ек
= 0; Еп = Е. Зеркальце будет отклоняться
до тех пор пока кинетическая энергия зеркальца Ек
не перейдёт в потенциальную энергию Еп =>
Ек = mзVз 2/2;
Еп = mзgh, где
mз - масса зеркальца, Vз -
скорость зеркальца, h - высота отклонения зеркальца.
Отсюда следует, что mзVз
2/2 = mзgh =>
Vз2 = 2gh (1). Импульс силы F
светового давления, действующей на тело, равен изменению
импульса тела: FдD t =
p2и-p1и =
mзVз-mз0 =
mзVз. FдD t =
mзVз (2). Величина давления лазерного
излучения: Pд = I/c(1+k) (3), где I -
интенсивность излучения, c - скорость света, k -
отражательная способность тела. В случае идеально отражающего
зеркальца (k=1): Pд=
I/c(1+1)= 2I/c. Интенсивность света: I =
E/SзDt. Тогда: Pд = 2I/c =
2E/cSзDt (4). Величина светового давления
Pд = Fд/Sз =>
Fд = PдSз. Тогда для силы
светового давления имеем: Fд =
2E/cDt (5). Из выражения (2) следует, что:
Vз = FдDt/mз. Подставим сюда выражение (5) для
скорости, приобретаемой зеркальцем под действием лазерного
излучения: Vз = 2E/cmз. Из
выражения (1) следует, что
(mз4E2/2c2mз2)
= mзgh => h =
2E2/gc2mз2
(6). Теперь, определим cos a, где a - угол отклонения зеркальца. Из
рисунка видно, что: cos a = 1-h/L, где L - длина нити, h
- высота отклонения зеркальца. Подставляя в это выражение
(6) получим:
cos a =
1-(2E2/gc2mз2L)=1-0.000038=0.999962,
a @ 0.5° .
2.13. Фотон с энергией Eф =
hn = hc/l = 60кэВ испытал комптоновское рассеяние на
покоившемся свободном электроне, в результате чего фотон
изменил своё направление движения и передал часть энергии
электрону, электрон изменил своё направление и получил импульс
ре, а энергия фотона уменьшилась. В соответствии с
этим, импульс рассеянного фотона станет: pф =
hn'. Тогда, согласно закону сохранения
энергии: hn = hn'+Еке, где Еке -
кинетическая энергия электрона отдачи, hn' - энергия рассеянного фотона. Из
этого выражения найдём Еке: Еке=
hn-hn' (1). Комптоновское смещение длины
волны рассеянного фотона: D l = l'-l = lк(1-cos q), где q - угол рассеяния фотона, длина волны
Комптона lк = 2ph /mc = 2.24610-12м. Длина волны рассеянного фотона:
l' = l'-l = lк(1-cos q), так как q =
1200
, то
cos1200 = 1/2 , и получим l' = l+lк/2. Тогда энергия рассеянного фотона:
Е' = hn' = hc/l' = hc/(l+lк/2). Затем рассеянный фотон выбивает
электрон из атома молибдена, т.е. происходит явление
фотоэффекта: hn' = Ek+Eсв =>
Ek = hc/(l+lк/2)-Eсв =
hc/(hc/E+lк/2)-Eсв = 36.9кэВ.
2.14. В результате комптоновского рассеяния
электрон и фотон разлетелись под углом 900 (см.
рис.2). Для решения задачи используем закон сохранения
энергии: hn = hn'+Eke, где hn - энергия налетающего фотона,
hn'- энергия рассеянного фотона; Исходя
из условия, что E' = Eke
получаем, что hn = 2hn', откуда: hc/l = 2hc/l' (1), то есть p = 2p',
тогда: l' = 2l (1'). Закон сохранения импульса будет
иметь вид: p = p'+pe => hn/c = hn'/c+meVe, где Ve – скорость
электрона. Выражение для комптоновского смещения:
Dl = l '-l = lk(1-cosq) или l '-l = lk(1-cosq). Подставим сюда выражение (1'):
2l -l = lk(1-cosq) => l = lk(1-cosq), l'-l'/2 = lk(1-cosq) => l' = 2lk(1-cosq) (2). Рассмотрим D ABC: cosq = p'/p = p'/2p' = 1/2 (3), cosq = 1/2 => q = 600. Используем выражение n = c/l, для того, чтобы найти импульс через
длину волны: p = hn/c = hc/lc = h/l, тогда p' = h/l' (4). Выразим из (3) значение импульса
p и получим: p = p'/cosq. Вместо p' подставим значение из
выражения (4): p = p'/cosq = h/l'cosq. В это выражение подставим значение
l' из (2) => p =
h/2lk(1-cosq)cosq => p = 2h/lk. Выполняя преобразования, получим:
lk = 2ph/mc, где h = h/2p. В результате имеем: p = 2mc =
54.648 10-23кг× м/с.

3. МОДЕЛЬ АТОМА
РЕЗЕРФОРДА - БОРА
3.1.
Мощность излучения электрона
равна убыли его полной энергии Е в единицу времени:
P = -dE/dτ. Отсюда “время жизни” атома
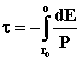 . Поскольку . Поскольку
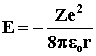 , то , то
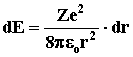 . Ускорение электрона . Ускорение электрона
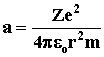 . Откуда . Откуда
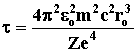 @ 6.5×10-11с. @ 6.5×10-11с.
3.2. Указание: 1) a- частица будет приближаться к тяжёлому
ядру Pb, пока она за счёт своей кинетической энергии
может "бороться" с кулоновскими силами, а затем
a- частица будет отброшена.
2) Сначала ядро лития покоится, а
затем, по мере приближения a- частица будет некоторое время
двигаться вместе с ядром лития (т.е. a- частица "бежит" за ядром лития).
Минимальное расстояние между ядрами будет, когда их скорости
станут одинаковыми.
3.9. Потенциал ионизации
Ui атома находится из уравнения
eUi = Ai, где
Ai - работа удаления электрона с
основной орбиты в бесконечность. Отсюда Ui =
hR/e = 13.6В.
Возможны 2 способа решения:
1) Ai - численно
равна энергии, поглощённой атомом при переходе из основного
состояния (n=1) в бесконечность: Ai =
E¥-E1 = 0-E1 =
-E1, где
E1 - энергия основного состояния атома
водорода. Тогда: Ui = Ai/e =
-E1/e.
2) Ai - численно
равна энергии, излучаемой атомом при переходе из бесконечно
удалённой орбиты в основное состояние: Ai =
hc/l = hcR(1/12-1/¥ 2) = hcR, где h - постоянная Планка,
c - скорость света, R - постоянная Ридберга.
Тогда: Ui = Ai/e = hcR/e =
13.6В.
3.13.
Кинетическая энергия электрона
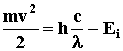 , где Ei -
энергия ионизации: , где Ei -
энергия ионизации:
Ei = hcR, тогда 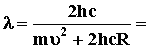 0.53×10-7 м.
0.53×10-7 м.
4.
ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
ГЕЙЗЕНБЕРГ
4.3. Классические представления о движении
частицы вдоль некоторой траектории должны в квантовой механике
применяться с учетом соотношения неопределенностей. По условию
задачи электрон движется в атоме, значит его положение может
быть определено с точностью
до размеров атома,
т.е. Dx ~ 10-10м. Говорить о
движении частицы по траектории имеет смысл лишь в тех случаях,
когда неопределенности в значениях скорости Dvх и координаты Dx, определяемые соотношением
Гейзенберга, значительно меньше, чем значения самой скорости
vх и координаты х. Рассчитаем
неопределенность в скорости из соотношения неопределенностей
Гейзенберга: Dрх×Dх ³ h, отсюда Dvх ~ h/(m×Dvх) ~ 106м/с, т.е.
Dvх ~ vх, значит, не имеет смысла говорить о
движении электрона в атоме по определенной траектории с точно
заданной в каждой точке скоростью.
4.7. Указание: l = h/mv = [h(1 - v2/c2)1/2]/mov, Ek = eU = [moc2/(1-v2/c2)1/2] - moc2. Отсюда l = h/[2moeU(1 + eU/2moc2)]1/2.
4.12.
Свободный электрон движется равномерно. Начальная область
локализации порядка размеров атома, а значит в этом случае
Dv ~ v, и соответственно: Dvo = Dv1 и Dx1 = Dv1×t. Из соотношения неопределенностей
Гейзенберга: Dv1 @ h/(m× Dx1). Тогда поскольку Dvo = Dv1, то Dx1/t @ h/(mDxo) и Dx1 @ ht/( mDxo)
=
1.2×106м.
4.13.
Dx @ hL/[d(2meU)1/2] =
0.78нм.
4.14.
Определим условие, при
выполнении которого ширина щели
b
будет будет обеспечивать минимальную ширину изображения на
экране. Ширина изображения (см. рис.) Х =
b
+2d.
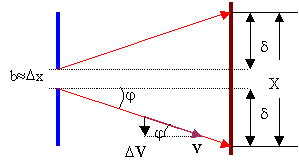
Условие минимальной ширины
изображения dX/db = 0 и отсюда можно определить искомое
значение ширины щели
b¢.
Атомы водорода, проходя через щель, отклоняются от
первоначального направления на некоторый угол
j. При этом импульс
частицы
p
приобретает некоторую неопределенность
Dрх
= 2Dр,
Dх
~
b.
Поскольку угол
j мал, то
tgj
=
d/L
~
sinj
~
Dр/p,
где L
– расстояние от щели до экрана. Таким образом,
d/L
~
Dрх/2p.
Из соотношения неопределенностей находим
Dрх
=
h/(Dх)
=
h/b
и получаем
d
~
Lh/2bр.
Тогда Х
@
b
+ Lh/bр
@
b
+ Lh/(bmHv).
Используем условие минимума Х и получаем dX/db = 1-
Lh/(b2mHv)
= 0, отсюда
b¢ = (Lh/mHv)1/2
= 10.24мкм.
5. ЭЛЕМЕНТЫ КВАНТОВОЙ
МЕХАНИКИ
5.2.
Уравнение Шредингера в области внутри ямы 0 <
x
<
l:
y¢¢(x)
+ k2y
= 0, k
= (2mE/h2)1/2.
Решение, удовлетворяющее
граничным условиям (y(0)
= 0,
y(l)
= 0), существует
лишь при таких значениях
k,
при которых
k
l =
np,
где n
= 1, 2, … Оно имеет вид:
y(x)
= A
sin(npx/l).
Постоянную А находим из условия нормировки:
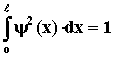
и нормированная волновая
функция будет иметь вид:
yn(x)
= (2/l)1/2×
sin
(npx/l).
Тогда вероятность
местонахождения частицы в области
l/3<
x
< 2
l/3
определится как
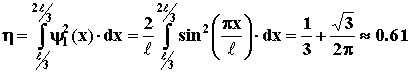 . .
5.4.
Плотность вероятности
местонахождения частицы в основном состоянии (n
= 1):
çY1÷2
= (2/l)×sin2(pa/x).
Максимальное значение плотности вероятности
çY1÷2
max
= 2/l
= Pm,
а значит
l
= 2/Pm
и E
= (phPm)2/8m.
5.11.
Указание:
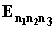 = [p2h2/(2ma2)]×(n12
+ n22 + n32) = A×(n12
+ n22 + n32); = [p2h2/(2ma2)]×(n12
+ n22 + n32) = A×(n12
+ n22 + n32);
а)
DE
= [p2h2/(ma2)];
б) Для 6-го уровня (n12+n22+n32)
= 14 и Е =
14А; число состояний равно 6 (число перестановок тройки чисел
1, 2, 3).
5.13.
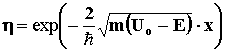 ;
h1
=
0.358; h2
=
0.0058; h3
=
3.4×10-5. ;
h1
=
0.358; h2
=
0.0058; h3
=
3.4×10-5.
5.17.
Решение уравнения Шредингера в
области х
³
0 имеет вид:
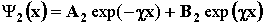 , где , где
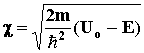 . Из требования конечности
Y2(х)
следует, что В2 = 0. Тогда . Из требования конечности
Y2(х)
следует, что В2 = 0. Тогда
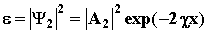 . По условию задачи
e(0)/e(хэф)
= e. Отсюда 2c×
хэф=1,
т.е. хэф=1/2c»0.1нм. . По условию задачи
e(0)/e(хэф)
= e. Отсюда 2c×
хэф=1,
т.е. хэф=1/2c»0.1нм.
6.
ЭЛЕКТРОННАЯ ОБОЛОЧКА АТОМА. МОЛЕКУЛЯРНЫЕ
СПЕКТРЫ
6.1. Энергия электрона En в атоме водорода (или
водородоподобном атоме) определяется величиной главного
квантового числа n (n = 1, 2, 3,…):
En = -
Z2me4/n28eoh2 =
ZE1/n2,
где Z - порядковый номер атома,
m - масса покоя электрона,
e - заряд электрона, eo - электрическая постоянная,
h - постоянная Планка, E1 = -13.56эВ энергия основного
состояния (n
= 1) атома
водорода.
Орбитальный момент импульса
Ml определяется величиной орбитального
квантового числа l, которое согласно теории
Бора-Зоммерфельда может принимать следующие значения:
l = 1, 2, …, n:
Ml = lh, где h = h/2p.
Магнитное
квантовое m (m=0, ±1, ±2, …, ±l) число дает
возможность определить величину проекции орбитального момента
MlH электрона на направление
внешнего магнитного поля:
MlH = mh.
А
спиновое квантовое число ms – проекцию
собственного механического момента (спина) электрона на
направление внешнего магнитного поля:
MsH = msh,
где
ms = ±1/2.
Тогда
суммарная величина проекции полного момента импульса будет
равна:
MH = (m+ ms)h.
6.12. Вращательная энергия двухатомной
молекулы определяется как:
EJ = J(J+1) h2/Io,
(1)
где
Io - момент инерции
молекулы, J - вращательное
квантовое число (J = 0, 1, 2,
3,…). В соответствии с (1): E2
- E1 = DE21 = hw21 = 2h2/Io, и E1 – Eo = DE10 = hw10 = h2/Io. Тогда согласно условию
задачи h(w21-w10)
= hDw = h2/Io, отсюда Io = h/Dw = 1.93×10-47
кг×м2 и поскольку
Io = mCmHr2/(mC+mH), где mC, mH - массы атомных ядер
углерода и водорода, входящих в молекулу, r - расстояние между ними, то r2 = Io(mC+mH)/ mCmH, а r =114пм.
7. РЕНТГЕНОВСКОЕ
ИЗЛУЧЕНИЕ
7.1. Указание: угол между первичным пучком
рентгеновских лучей и отраженным в два раза больше угла
скольжения, входящего в формулу Вульфа-Брэггов.
7.4.
Наблюдаемое явление – дифракция
электронов на монокристалле алюминия, возможная благодаря
наличию волновых свойств у электронов.
По условию:
U1/Uo
=
h = 2.25
(1)
Длина волны де Бройля
электронов при ускоряющем напряжении
Uo:
lо
= h/pо = h/(2meUо)1/2
(2), а при ускоряющем напряжении
U1:
l1
= h/p1 = h/(2meU1)1/2
(3), Из (2) и (3) следует, что отношение
lо/l1
= (U1/Uо)1/2
(4), Условие Вульфа - Брэггов появления максимумов запишется
как: 2dsinQ
= nоlо
и 2dsinQ
= n1l1
(5), где n1 и nо – порядок
отражений. Из (5) видно, что
nоlо
= n1l1
или
lо/l1
= n1/nо
(6), Согласно условию задачи
n1
= nо+1,
тогда из (6) получаем:
lо/l1
= (U1/Uо)1/2-1
(7)
Следовательно:
nо = 1/(h1/2-1).
(8)
Используя 1-е выражение (5) и
(8), получаем:
2dsinQ
=
lо/(h1/2-1).
(9)
Отсюда, учитывая (2), имеем:
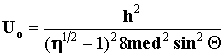 = 37В. = 37В.
7.7. Указание: учесть, что v ~ c, а значит, масса электронов будет
зависеть от скорости.
7.9. Согласно закону Мозли частота
излучения, соответствующая Кa-линии характеристического
рентгеновского спектра, определяется как:
nКa = Rc(Z - 1)2(1 –
1/4),
отсюда находим lКa = 0.072нм. Для того, чтобы узнать,
можно ли получить эту линию спектра при U = 4кВ,
необходимо сравнить энергию, которую необходимо затратить на
удаление электрона с К-оболочки молибдена
(Е1 = hRc(ZMo-1)2) с энергией электронов, которую они
приобретают в рентгеновской трубке (Е2 =
eU). Поскольку Е2
< Е1, то в этом случае нельзя получить
Кa - линию характеристического
спектра.
7.10.
Энергия кванта Кa меди E1 = hnКa = hRc(ZСu- 1)2(1 –
1/4), а энергия,
необходимая для вырывания электрона с К-оболочки
марганца (т.е. энергия связи К-электронов):
E2 = hRc(ZMn - 1)2. Отсюда кинетическая энергия
электронов:
Ek =
hRc[(Zcu - 1)2 ×3/4 - (ZMn -
1)2] = 0.16кэВ.
8. СТРОЕНИЕ
АТОМНОГО ЯДРА. ДЕФЕКТ МАССЫ.
ЭНЕРГИЯ СВЯЗИ ЯДРА. ЯДЕРНЫЕ
РЕАКЦИИ
8.1. Ядро атома гелия состоит из 2
протонов и 2 нейтронов. При синтезе атома гелия дефект массы
Dm = 2(mp + mn) -
MHe, и
энергия, выделяющаяся при этом DЕ = Dm×931MэВ. При синтезе 1г гелия выделится
энергия Е = DЕ×N, где N - число атомов в
1г гелия. Е = 42.56×1023МэВ.
8.4. Указание: необходимо найти энергию,
которую надо затратить, чтобы нейтрон или a-частица покинули ядро
11В5, т.е. произошли следующие
ядерные реакции:
1: 11
В 5® 10 В 5 + 1
n 0,
2: 11
B 5® 7 Li 3 + 4
He 2.
8.7. Освобождающаяся при ядерных реакциях
энергия равна разности между суммарной энергией связи
образовавшихся ядер и суммарной энергией связи исходных ядер:
DЕ = e (12С6)+
e (4Не2)-
e (14N7) = 4.9МэВ, реакция идет с
выделением тепла.
8.9.
Согласно условию задачи mavao
= 2mavacosj
= 2mxvxcosj
(1). Из закона сохранения энергии
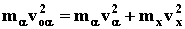 (2). (2).
Выражая из (1) значения va
и va,
получаем
va=
mavao/2mxvxcosj
(3),
va
= vao/2cosj
(4).
Подставляя полученные значения
в (2), имеем
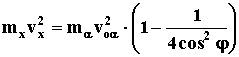 , и т.к. с учетом (3) , и т.к. с учетом (3)
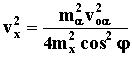 , то , то
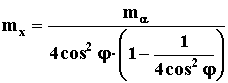 . При
j
= 30°, mx = ma/2,
т.е.
a-
частица столкнулась
с ядром дейтерия. . При
j
= 30°, mx = ma/2,
т.е.
a-
частица столкнулась
с ядром дейтерия.
8.10.
Необходимо учесть,
что любая ядерная реакция происходит с выделением или
поглощением энергии, поэтому закон сохранения энергии в
данном случае запишется как
Ep+DЕ
= 2Ea,
где Ep
= Е - кинетическая
энергия протона,
DЕ
– энергия ядерной реакции,
Ea
- кинетическая энергия альфа-частиц.
DЕ
= (mLi
+ mp
– 2m
a)c2,
Ea
= (m
a va2)/2.
Учтя, что
cos(a/2)
= (m
p vp)/(2ma
va),
в результате получаем
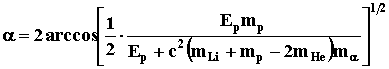 . .
8.13.
Находим общее число
актов деления, необходимых для получения энергии, равной
P×t/h. Оно равно (P×t)/ /(h×e), где e - энергия, выделившаяся в одном акте.
Тогда общий расход 235U равен
mU×(P×t/h×e), где mU - масса
атома 235U. Расход равен 72×10-3кг.
8.14.
Увеличение количества нейтронов при работе реактора за время
dt равно dn = [n(k -1)×dt]/T. Отсюда n/no =
exp[t(k -1)/T] = 1.016. Для n/no = e,
получим tp = T/(k - 1) = 30c.
9. ЕСТЕСТВЕННАЯ
РАДИОАКТИВНОСТЬ
9.1.
Указание: число атомов в m = 0.248×10-6кг натрия
определяется как N0 = m×NA/A, где NA – число Авогадро, А – молярная
масса (АNa = 25 кг/кмоль).
9.4.
По закону
радиоактивного распада N =
Noexp(-lt), l = ln2/T - постоянная распада, Т –
период полураспада. Доля оставшихся ядер N/No = exp(-lt) = exp(-ln2t/T) =
2-t/T. Доля распавшихся ядер
(No – N)/No = 1 – 2-t/T. Поскольку период полураспада
стронция составляет 28 лет и в
этом случае Dt << T, то для нахождения доли атомов,
распавшихся за одни сутки, необходимо использовать
дифференциальную форму закона радиоактивного распада dN =
-lNodt, а доля распавшихся атомов
(No – dN)/No = 1 -
ldt =
1 - (t×ln2)/T.
9.6.
По закону радиоактивного распада N =
Noexp(-lt), l = ln2/T - постоянная распада. N = No -
DN =
Noexp(-t×ln2/T) =
No2-t/T. Отсюда DN1 =
No - No 2-Dt/T= 7.3×1018
атомов. Dt2 = 1с и Dt2/T = 81×10-8 » 0, поэтому в случае
Dt << T, необходимо использовать
дифференциальную форму закона радиоактивного распада: dN =
-lNodt, тогда DN2=lNoDt2 =
No(ln2/T)Dt2 = 1.1×1013 атомов.
9.9.
Пусть руда образовалась Т
(период полураспада 238U92) лет
тому назад. К моменту времени t (отсчет ведется от
нынешнего момента времени) распалось
DN
=
No.{1 -
exp×[-ln2(T
- t)/T]} и осталось
N = Noexp[-ln2(T - t)/T] атомов урана.
Значит, отношение числа атомов урана t = 109
лет тому назад было:
 =0.72. =0.72.
10. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
10.7.
На основе законов сохранения энергии и импульса находим где E1 и E2 – энергии g-квантов. Отсюда видно, что Tmin будет при E1 = E2 = (mp + Ekp)/2 = mp. Таким образом, Tmin = 60.
|