|
Решения
и указания к решениям избранных задач
1. ЭКСПЕРИМЕНТАЛЬНЫЕ
ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ.
МОДЕЛЬ АТОМА РЕЗЕРФОРДА. ТЕОРИЯ АТОМА ВОДОРОДА ПО БОРУ.
2. ВОЛНОВЫЕ
СВОЙСТВА МИКРОЧАСТИЦ.
СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ГЕЙЗЕНБЕРГА.
3. УРАВНЕНИЕ
ШРЕДИНГЕРА ДЛЯ СТАЦИОНАРНЫХ СОСТОЯНИЙ.
4. ОПЕРАТОРЫ
И ИХ СВОЙСТВА.
5. ОПЕРАТОРЫ
ФИЗИЧЕСКИХ ВЕЛИЧИН.
ОПЕРАТОР МОМЕНТА ИМПУЛЬСА В СФЕРИЧЕСКИХ КООРДИНАТАХ.
6.
ИНТЕГРАЛЫ ДВИЖЕНИЯ.
7.
ЛИНЕЙНЫЙ ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР.
8. ДВИЖЕНИЕ
В ЦЕНТРАЛЬНОМ ПОЛЕ.
1.2. В данной задаче необходимо учесть, что под
энергией стационарного состояния атома понимается сумма
кинетической энергии вращения электрона вокруг ядра и
потенциальной энергии кулоновского взаимодействия электрона
с ядром:

 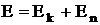
При движении электрона по круговой орбите роль
центростремительной силы играет кулоновская сила. Тогда
имеем :
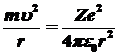 , ,
где
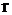 -
расстояние электрона от ядра или радиус боровской орбиты, -
расстояние электрона от ядра или радиус боровской орбиты,
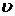 -
линейная скорость движения электрона, -
линейная скорость движения электрона,
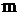 -
масса электрона, -
масса электрона,
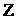 -
заряд ядра. -
заряд ядра.
Преобразуем данную формулу:
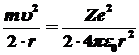 ,
отсюда ,
отсюда 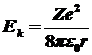 , ,
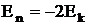
Радиус
первой боровской орбиты:
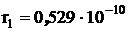 м, м,
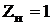 . .
Тогда:
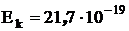 Дж= Дж=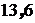 Эв Эв
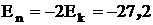 Эв, Эв,
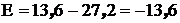 (Эв). (Эв).
1.4. Для решения
данной задачи необходимо использовать правило частот и
выражение энергии для водородоподобных атомов:
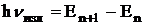 , ,
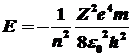
Частота излучения
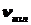 при
переходе электрона с при
переходе электрона с
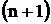 орбиты
на орбиты
на 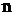 -ю
равна: -ю
равна:
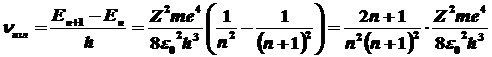 , ,
а для 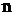 >>1
имеем: >>1
имеем:
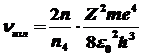 , ,
Линейная частота
обращения:
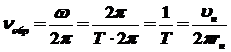 , ,
т.к. период обращения
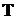 равен: равен:
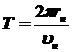 ,
где ,
где 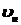 -
скорость движения электрона по стационарной орбите. -
скорость движения электрона по стационарной орбите.
Поскольку
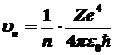 , ,
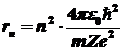 ,
то ,
то 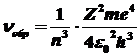 , ,
следовательно,
nизл
=nобр.

2.1.
Первый
способ решения:
1) По условию задачи электрон
движется в атоме, значит
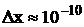 м. м.
Согласно СНГ:
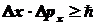 , ,
тогда неопределенность
значения проекции импульса
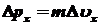 , ,
следовательно,
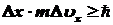 , ,
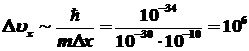 (м/с), (м/с),
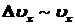 , ,
т.е. в данном случае понятие
траектории электрона, движущегося в атоме, не имеет смысла.
Говорить о движении частицы по траектории имеет смысл лишь в
том случае, когда неопределенность в значении скорости
 ,
определенное СНГ, значительно меньше, чем значение самой
скорости ,
определенное СНГ, значительно меньше, чем значение самой
скорости 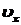 ,
т.е. ,
т.е. 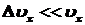 . .
Второй способ решения:
2) Волновые свойства будут
проявляться в том случае, если длина волны де Бройля будет
порядка области движения частицы. Так как электрон находится
в атоме, то 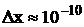 м.
Мы можем рассчитать длину волны де Бройля электрона в атоме
и сравнить ее с м.
Мы можем рассчитать длину волны де Бройля электрона в атоме
и сравнить ее с 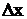 : :
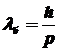 , ,
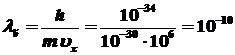 (м), (м),
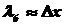 . .
В данном случае размеры
области движения частицы не велики по сравнению с ее де
Бролевской волной, поэтому говорить о траектории электрона,
движущегося в атоме, не имеет смысла.
2.5. Так как атомы
водорода обладают волновыми свойствами, то при прохождении
их через щель будет наблюдаться дифракционная картина.
Вследствие дифракции частицы отклоняются от первоначального
положения (см. рис.). Следовательно, появляется
неопределенность в значении импульса вдоль оси ОХ.
При этом ширина изображения :
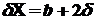 , ,
где
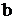 -
ширина щели; -
ширина щели; 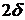 -
дополнительное уширение, связанное с неопределенностью
импульса -
дополнительное уширение, связанное с неопределенностью
импульса 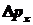 . .

Условие
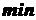 ширины
изображения: ширины
изображения:
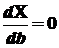 . .
Неопределенность импульса
частицы
 , ,
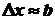 .
Так как угол .
Так как угол
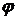 отклонения
частицы от первоначального направления отклонения
частицы от первоначального направления
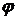 достаточно
мал, то достаточно
мал, то
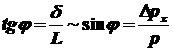 , ,
где
L
– расстояние от щели до экрана. Таким образом,
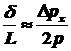 . .
Из СНГ:
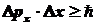 ,
т.е. ,
т.е.  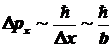 ,
следовательно, ,
следовательно,
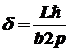 ,
тогда ширина изображения ,
тогда ширина изображения 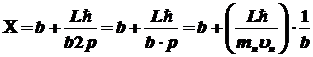 
Используя условие
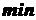 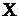 ,
получаем ,
получаем
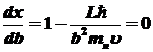 ,
отсюда ,
отсюда
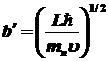 . .
2.7. В данной задаче
необходимо учесть, что неопределенность в импульсе связана с
неопределенностью в координате соотношением
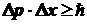 .
В данном случае .
В данном случае
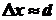 ,
где ,
где
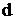 -
межплоскостное расстояние -
межплоскостное расстояние
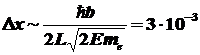 (м), (м),
где
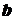 -
диаметр дифракционного кольца, -
диаметр дифракционного кольца,
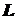 -
расстояние от фольги до экрана, -
расстояние от фольги до экрана,
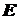 -
энергия, -
энергия,
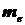 -
масса электрона. -
масса электрона.

3.3. Состояние
частицы, находящейся в основном состоянии (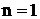 )
в прямоугольной потенциальной яме шириной )
в прямоугольной потенциальной яме шириной
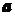 описывается
волновой функцией: описывается
волновой функцией:
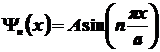 , ,
где
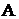 -
коэффициент нормировки. -
коэффициент нормировки.
Плотность вероятности
нахождения частицы внутри ямы:
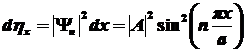 , ,
отсюда вероятность
нахождения частицы в области
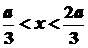 будет: будет:
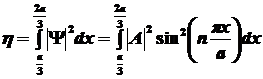
Чтобы найти вероятность
нахождения частицы в заданной области, необходимо сначала
вычислить коэффициент нормировки
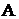 .
Для этого воспользуемся условием нормировки для частицы в
яме ( .
Для этого воспользуемся условием нормировки для частицы в
яме (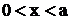 ): ):
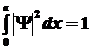 , ,
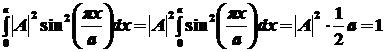 , ,
при расчете интеграла
необходимо учесть, что
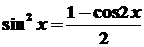 . .
Значит
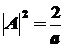 , ,
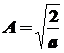 . .
Теперь найдем вероятность
обнаружения частицы в заданной области
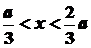 : :
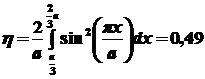 . .
3.4. В результате
решения одномерного уравнения Шредингера, описывающего
движение частицы в областях
I
и II,
получены волновые функции. Нас интересует поведение частицы
за барьером, а там состояние частицы соответствует волновой
функции:
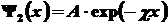 ,
где ,
где
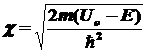
Плотность вероятности
нахождения частицы за барьером определяется квадратом модуля
волновой функции:
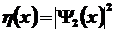 , ,
по условию задачи
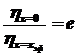 ,
иначе ,
иначе
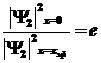 , ,
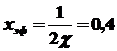 (нм) (нм)
3.5. В данной задаче
необходимо учесть, что соотношение коэффициентов отражения и
прохождения можно выразить следующей формулой:
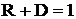 . .

4.4.
По условию
задачи 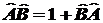 или или
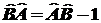 ,
тогда: ,
тогда:
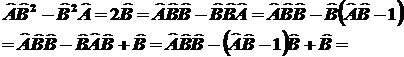  . .
4.6. Оператор
комплексного сопряжения
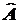 преобразует
функцию F в комплексно сопряженную
F *: преобразует
функцию F в комплексно сопряженную
F *:
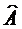 F=F
*. F=F
*.
4.7. Уравнение на
собственные функции оператора
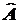 следующее: следующее:
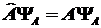 . .
Находим результат действия
оператора 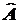 на
функцию на
функцию 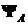 : :
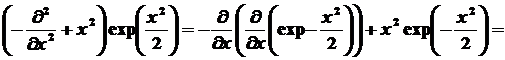 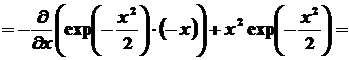 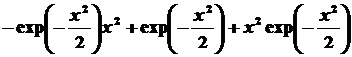 . .
Таким образом, получаем:
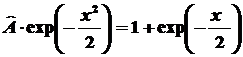 ,
следовательно А=1. ,
следовательно А=1.

5.1. Оператор
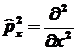
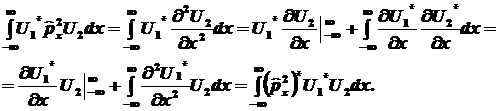
5.4. Оператор
Лапласа:
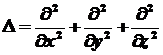 . .
5.5. См. [10], стр.
197.
5.10. Оператор
квадрата момента импульса
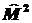 в
сферических координатах: в
сферических координатах:
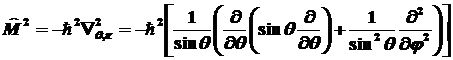 . .
Собственные функции
оператора 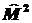 : :
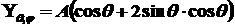 , ,
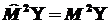 . .

ИНТЕГРАЛЫ ДВИЖЕНИЯ.
6.1. Для свободно
движущейся частицы потенциальная энергия
U(x,
y,
z,
t)=0.
Полная энергия 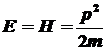 ,
а значит ,
а значит 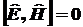 ,
т.е. полная ,
т.е. полная
энергия свободнодвижущейся частицы интеграл
движения.
Для выяснения будут ли
интегралами движения операторы
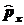 , ,
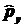 , ,
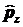 необходимо
определить, чему равны коммутаторы операторов этих величин с
оператором Гамильтона данной системы необходимо
определить, чему равны коммутаторы операторов этих величин с
оператором Гамильтона данной системы
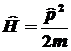 .
Например: .
Например:
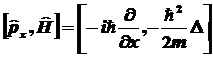 . .
Находим результат действия
первого члена коммутатора на некоторую функцию
f:
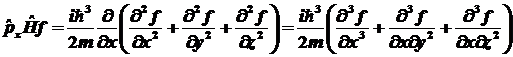 . .
Затем аналогично для второго
члена:
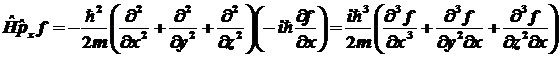 . .
Поскольку
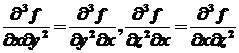 ,
то ,
то 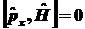 ,
т.е. ,
т.е. 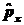 - -
интеграл движения.
Для установления является ли
оператор квадрата момента импульса
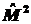 интегралом
движения, необходимо найти коммутатор интегралом
движения, необходимо найти коммутатор
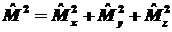 и и
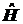 . .
Задачу можно решать как в
декартовых, так и в сферических координатах.
6.2. В данной задаче
необходимо определить коммутируют ли операторы
соответствующей величины с оператором
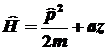 . .
6.3. Для решения
задачи удобно использовать выражения для операторов
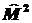 , ,
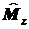 , ,
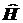 в
сферических координатах. Поскольку эти операторы явно от
времени не зависят, то для сохранения в
сферических координатах. Поскольку эти операторы явно от
времени не зависят, то для сохранения
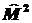 , ,
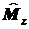 необходимо,
чтобы необходимо,
чтобы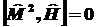 и и
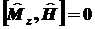 .
А значит, следует .
А значит, следует
выяснить, при каких условиях эти операторы
обращаются в ноль.
Рассмотрим решение задачи
для оператора 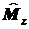 : :
 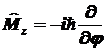 , ,
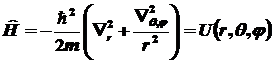 . .
Первый член коммутатора
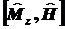 : :
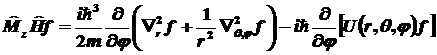 (1).
(1).
Второй член:
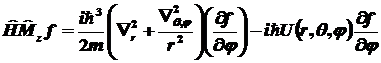 (2).
(2).
Первые члены в (1)и (2) равны, а значит для того, чтобы
коммутатор был равен нолю, необходимо, чтобы
 (3).
(3).
(3) будет выполняться, если
потенциальная энергия системы не будет зависеть от
 ,
т.е. ,
т.е.  . .

7.
ЛИНЕЙНЫЙ ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
7.1. Рассмотрим
решение для состояния
n=0.
В этом случае  и,
подставив значение и,
подставив значение
 в
уравнение в
уравнение
Шредингера для гармонического осциллятора, будем
иметь для первого члена уравнения:
 . .
Соответственно уравнение преобразуется к виду:
 . .
Так как
 ,
то получаем: ,
то получаем:
 . .
Для выполнения равенства должно быть:
 ,
т.е. ,
т.е.  или или
 ,
окончательно ,
окончательно  . .
7.2. Найдем
нормировочный коэффициент для первого состояния
гармонического осциллятора (n=0).
Учтем, что  и и
 ,
тогда ,
тогда . .
Условие нормировки для
волновой функции:
 , ,
следовательно:
 (1).
(1).
Рассмотрим значение
интеграла левой части (1):
 . .
Используя замену переменной
 ,
приводим интеграл к ,
приводим интеграл к
табличному (см. теор. введение к
разделу). Поскольку
 , ,
 , ,
 , ,
то имеем
  . .
И наконец, так как
 ,
то ,
то  ,
а нормировочная ,
а нормировочная
волновая функция первого состояния
гармонического осциллятора:
 . .
7.4. а) Среднее
значение  согласно
постулату о среднем значении равно: согласно
постулату о среднем значении равно:
 . .
Учитывая, что
 , ,
можно привести интеграл к
табличному, проведя стандартную замену переменной
 .
Тогда будем иметь .
Тогда будем иметь
 . .
7.5. Вероятность
нахождения частицы, движущейся под влиянием квазиупругой
силы, вне границ, дозволенных классической механикой:


8.1. Для состояния
1s:
n=1,
l=1,
m=0,
а  . .
Для нахождения собственного
значения энергии атома водорода в состоянии 1s
(Е1)
необходимо использовать радиальное уравнение Шредингера:
 . .
Учтем, что
 ,
а
l=0: ,
а
l=0:
 . .
Проведя необходимые
преобразования, получаем:
 или или
 . .
Иначе
 . .
Для выполнения равенства необходимо, чтобы
 и и
 . .
Отсюда следует:
 и и
 . .
8.3. Условие
нормировки радиальной части волновой функции:
 . .
Используя замену переменной
 ,
приводим интеграл к табличному ,
приводим интеграл к табличному
виду (см. теор. введение
раздела). После ряда преобразований будем иметь:
 и и
 . .
8.4. Для 1s
– состояния
n=1,
l=0,
 . .
 , ,
 , ,
 . .

|