3.1. Написать уравнение
Шредингера:
а) для частицы, движущейся под действием квазиупругой силы;
б) для заряженной частицы, движущейся в
кулоновском поле ядра.
3.2. Доказать, что энергия
свободно движущейся частицы может иметь любые значения
(непрерывный спектр собственных значений энергии).
3.3. Частица находится в
основном состоянии в прямоугольной потенциальной яме шириной
a с абсолютно непроницаемыми стенками (0<x<a).Найти
вероятность местонахождения этой частицы в области a/3<x<2a/3.
3.4. Частица массы m
падает слева на прямоугольный потенциальный барьер высотой
Uo. Энергия частицы равна Е,
причем Е<Uo. Найти эффективную глубину
xэф проникновения частицы под барьер, т.е.
расстояние от границы барьера до точки, в которой плотность
вероятности
e
нахождения частицы уменьшается в "е" раз. Вычислить
xэф
для электрона, если Uo-E=1
эВ.
3.5. Показать, что
коэффициент прозрачности потенциального барьера для частиц
с энергией Е<Uo равен нулю.
3.6. Частица падает слева
на прямоугольный потенциальный барьер высотой Uo
, причем E>Uo. Доказать, что в точке
x=0 происходит частичное отражение волны. Подсчитать
коэффициент отражения.
3.7. Найти выражение для
вероятности прохождения микрочастицы с энергией E<Uo
сквозь потенциальный барьер конечной ширины "а".

4.1. Доказать, что
операторы x и
¶/¶y,
y и
¶/¶x,
x и
¶/¶z
и вообще операторы "независимая переменная " и
"дифференцирование по другой независимой переменной"
коммутируют.
4.2. Доказать, что результат
применения оператора (¶/¶x
× x)2
к функции sin x есть функция (sinx + 3x
×
cosx), а
результат применения оператора (x
¶/¶x)2
к той же функции есть (x
×cosx
- x2
×sinx).
4.3. Пусть
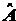 =
¶/¶x,
=
¶/¶x,
 =
x. Вычислить разность
=
x. Вычислить разность
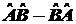 ,
применяя ее к произвольной функции
Y.
Показать, что
,
применяя ее к произвольной функции
Y.
Показать, что
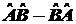 =
1.
=
1.
4.4. Пользуясь алгеброй
операторов, доказать, что если
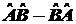 =1,
то а)
=1,
то а) 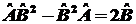 , б)
, б)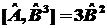
4.5. Доказать, что оператор
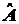 =
(¶/¶x+x)2
не равен
квадрату суммы величин, стоящих в скобках.
=
(¶/¶x+x)2
не равен
квадрату суммы величин, стоящих в скобках.
4.6. Является ли оператор
комплексного сопряжения: а) линейным, б) эрмитовским, в)
чему равен оператор комплексного сопряжения от оператора
комплексного сопряжения?
4.7. Доказать, что еxp
(-х2/2) есть собственная функция оператора
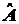 =
-¶2/¶x2+x2,
принадлежащая собственному значению 1, а x×
exp(-x2/2)
есть собственная функция того же оператора, принадлежащая
собственному значению 3.
=
-¶2/¶x2+x2,
принадлежащая собственному значению 1, а x×
exp(-x2/2)
есть собственная функция того же оператора, принадлежащая
собственному значению 3.
4.8. Доказать эрмитовость
операторов: a) 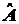 =x,
b)
=x,
b) 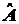 =
¶/¶x, c)
=
¶/¶x, c)
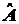 =
-¶2/¶x2.
=
-¶2/¶x2.
4.9. Оператор
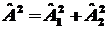 .
Доказать, что если операторы
.
Доказать, что если операторы
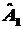 и
и
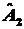 коммутируют
с оператором
коммутируют
с оператором
 ,
то с ним коммутирует и оператор
,
то с ним коммутирует и оператор
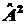
4.10. Найти собственные
значения оператора
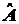 ,
принадлежащие собственной функции
yА,
если:
,
принадлежащие собственной функции
yА,
если: 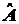 =d2/dx2+(2/x)(d/dx),
yА
=(sinax)/x.
=d2/dx2+(2/x)(d/dx),
yА
=(sinax)/x.
4.11. Найти собственную
функцию
y
и собственное значение оператора
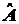 =
-i×(¶/¶x),
если
y(х)=y(х+а),
где а - постоянная величина.
=
-i×(¶/¶x),
если
y(х)=y(х+а),
где а - постоянная величина.
4.12. Проверить следующее
равенство для коммутатора:
[x2,[x,-h2׶2/¶x2]]=
-4h2х.

5.1. Доказать эрмитовость
следующих операторов:
а)
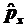
;
б) 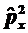 ;
;
в) 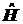 .
.
5.2. Проверить следующие
равенства для коммутаторов:
а)
[f(x),
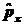 ]
= iћ(¶f/¶x);
]
= iћ(¶f/¶x);
б)
[f(x),
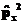 ]
=
2iћ(¶f/¶x)×
]
=
2iћ(¶f/¶x)×
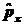 +ћ2(¶2f/¶x2),
+ћ2(¶2f/¶x2),
здесь f(x)-
произвольная функция координаты.
5.3. Проверить следующие
правила коммутации для гамильтониана
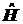 в
потенциальном поле U(x):
в
потенциальном поле U(x):
а) [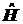 ,
x]=- (iћ/m)
,
x]=- (iћ/m)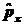 ;
;
б) [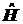 ,
,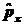 ]=iћ(¶U/¶x);
]=iћ(¶U/¶x);
в) [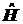 ,
,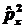 ]=2iћ(¶U/¶x)×
]=2iћ(¶U/¶x)×
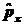 +ћ2(¶2U/¶x2).
+ћ2(¶2U/¶x2).
5.4. Найти коммутатор
оператора x и оператора Лапласа.
5.5. Найти выражение
оператора 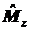 в сферической системе координат.
в сферической системе координат.
5.6. Проверить следующие
правила коммутации:
а)
[x,
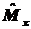 ]
= 0;б)
[y,
]
= 0;б)
[y,
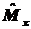 ]
=-iћz
; в)[z,
]
=-iћz
; в)[z,
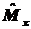 ]=iћy.
]=iћy.
5.7. Доказать следующие
правила коммутации :
а)
[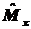 ,
,
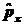 ]=0;
б)[
]=0;
б)[ 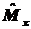 ,
,
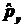 ]=iћ
]=iћ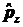 .
.
5.8. С помощью правил
коммутации, приведенных в предыдущей задаче, показать, что
[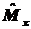 ,
,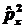 ]=0.
]=0.
5.9. Проверить следующее
правило коммутации: [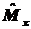 ,
,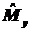 ]=iћ
]=iћ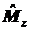 .
.
5.10. Найти собственные
значения оператора квадрата момента импульса
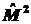 ,
соответствующие его собственной функции:
,
соответствующие его собственной функции:
Y(q,j)=A(cosq+2sinq×cosj).
5.11. Доказать эрмитовость
оператора x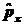 .
.
5.12. Доказать, что оператор
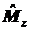 эрмитов.
Доказательство провести в декартовых координатах.
эрмитов.
Доказательство провести в декартовых координатах.
5.13. Доказать эрмитовость
оператора 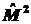 ,
имея в виду, что операторы
,
имея в виду, что операторы
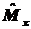 ,
,
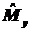 ,
,
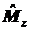 эрмитовы
.
эрмитовы
.
5.14. Найти среднее значение
координаты частицы в одномерной прямоугольной потенциальной
яме с абсолютно непроницаемыми стенками и шириной
l,
если частица находится в основном состоянии, описываемом
волновой функцией
y1(x)=(2/l)1/2×sin(px/l).
5.15. Найти среднюю
кинетическую энергию частицы в одномерной прямоугольной
потенциальной яме с абсолютно непроницаемыми стенками (0<х<а),
если частица находится в состоянии: а)
y(x)=A×sin2(px/a);
б)
y(x)=A×x×(a-x).
5.16. Определить среднее
значение физической величины, описываемой оператором
 в
состоянии
y(j)=A×sin2j
.
в
состоянии
y(j)=A×sin2j
.

ИНТЕГРАЛЫ ДВИЖЕНИЯ.
6.1. Выяснить будут ли
сохраняться проекции импульса, энергия, проекции и квадрат
момента импульса при свободном движении частицы.
6.2. Какие из механических
величин (энергия Е, проекции импульса, проекции и
квадрат момента импульса) сохраняются при движении частицы
в однородном потенциальном поле U(z)=az (где а-
постоянная)?
6.3. Определить, при каких
условиях квадрат момента импульса М2
и его проекция Мz могут быть
интегралами движения.

7.1. Получить собственные
значения энергии гармонического осциллятора в первых двух
состояниях (n=0 и
n=1)
непосредственной подстановкой в уравнение Шредингера:
d2Y(x)/dx2
+ (e-x2)×Y(x)
соответствующих собственных
функций
Yo(x)
= Co×exp(-x2/2)
и
Y1(x)=
C1×2x×exp(-x2
/2).
7.2. Найти нормировочные
коэффициенты собственных функций гармонического осциллятора
для первых двух состояний.
7.3. Пользуясь выражениями
для нормированных собственных функций гармонического
осциллятора, вычислить средние значения
<x>
и
<x2>
для двух первых состояний, n=0 и n=1.
7.4. Волновая функция
основного состояния гармонического осциллятора имеет вид:
Yo(x) =
(a/Öp)1/2×exp(-a2x2/2),
где
a=(mw/ћ)1/2
(m-масса,
w-
собственная частота осциллятора). Энергия осциллятора
в этом состоянии
Eo=ћw/2.
Найти:
а) среднее значение
модуля координаты <|x|>,
б) выразить <|x|>
через классическую амплитуду а, которая связана с
энергией осциллятора соотношением E=mw2a2/2,
в)среднее значение
потенциальной энергии осциллятора
<U>.
7.5. Волновая функция для
частицы, движущейся под влиянием квазиупругой силы, имеет
вид:
Yo(x)
=(mw/pћ)1/4×exp(-mwx2/2ћ)
Вычислить для данного
состояния вероятность нахождения частиц вне границ,
дозволенных классической механикой.

8.1. Определить собственное
значение энергии En атома
водорода в 1s состоянии, собственная функция которого
сферически симметрична: R(r)= A×exp(-ar).
8.2. Собственная функция
1s - состояния атома водорода имеет вид
Y(r)=
A×exp(-r/r1),
где r1 - первый боровский радиус.
а) Определить вероятность
нахождения электрона на расстоянии от r до r+dr
от ядра в данном состоянии;
б) На каком расстоянии от ядра электрон будет находиться с
максимальной вероятностью?
8.3. Найти выражение для
нормированной собственной функции атома водорода в 1s-состоянии,
учтя, что R10(r)= A×exp(-r/r1).
8.4. Определить среднее
значение радиуса
<r>
и среднее значение потенциальной и кинетической энергии
атома водорода в 1s-состоянии.
8.5. Какова кратность
обязательного вырождения для 3d и 4f-состояний
электрона в атоме водорода?
8.6. Найти величины момента
импульса М и проекции момента импульса на ось z
Mz для электрона в атоме водорода в
состояниях 1s, 3d, 4f.
