В классической механике
движение частиц описываются с помощью уравнения Ньютона:
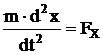
Наличие волновых свойств
микрочастиц делает невозможным применимость уравнения
Ньютона. Для описания движения микрочастиц, необходимо
использовать уравнение, учитывающее не только
корпускулярные, но и волновые свойства частиц. Таким
является основное уравнение квантовой механики - уравнение
Шредингера.
Уравнение Шредингера - это
уравнение относительно волновой функции, физический смысл
которой заключается в том, что квадрат модуля волновой
функции определяет вероятность нахождения частицы в данной
точке пространства в данный момент времени.
Временное уравнение
Шредингера:
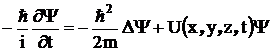 ,
,
где
Y=Y(x,
y,
z,
t)
- волновая функция,
U(x,
y,
z,
t)
- потенциальная энергия частицы.
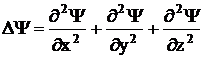 - лапласиан
Y.
- лапласиан
Y.
Волновая функция
Y
удовлетворяет следующим условиям, всюду непрерывна и имеет
непрерывные первые производные, однозначна и конечна во всем
пространстве.
В случае одномерного
движения частицы в потенциальном поле
U(x)
стационарное уравнение Шредингера записывается в виде:
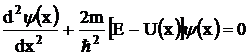 ,
,
где Е - полная
энергия частицы,
y
=
y(x)
- координатная часть волновой функции.
Движение свободной микрочастицы
При движении свободной
частицы (U(x)=0)
ее полная энергия совпадает с кинетической. Для свободной
частицы, движущейся вдоль оси х уравнение Шредингера
для стационарных состояний примет вид:
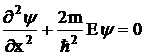 или
или
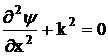 ,
,
где
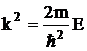 .
.
Для свободной частицы
волновая функция представляет собой суперпозицию двух
плоских монохроматических волн, распространяющихся в
противоположных направлениях.
Этому соответствует
независящая от времени плотность вероятности обнаружения
частицы в данной точке пространства:
|Y|2=YY*=|A|2.
Для свободно движущейся
частицы энергия определяется из формулы:
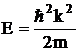 ,
,
так как на
k
не накладываются ограничения, то энергия может принимать
любые значения, т. е. энергетический спектр свободно
движущейся частицы сплошной.
Движение микрочастицы в бесконечно глубокой
потенциальной яме
При изучении одномерного
движения микрочастицы в бесконечно глубокой потенциальной
яме, потенциальная энергия частицы имеет вид:
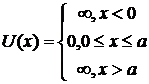
Решение стационарного
уравнения Шредингера в этом случае дает следующую волновую
функцию:
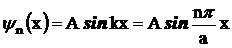 ,
,
где
a
- ширина ямы,
A
- постоянная нормировки, получаемая из требования нормировки
волновой функции:
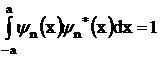

В этом случае энергетический
спектр микрочастицы является дискретным, энергия может быть
найдена как:
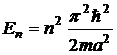 ,
,
где
n=1,
2, …¥
- квантовое число, определяющее энергию частицы в яме.
Расстояние между соседними
энергетическими уровнями:
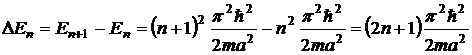 ,
,
т.е. с ростом
n
происходит относительное сближение энергетических уровней.
Плотность вероятности
местонахождения частицы внутри ямы:
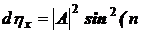
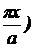
зависит от местонахождения
частицы.
Прохождение частицы
через потенциальный барьер.
Туннельный эффект
Рассмотрим движение
микрочастицы массы
m
с энергией
E
в пространстве, в котором силовое поле меняется следующим
образом (см. рис.).

Потенциальная энергия
частицы в области
I
(-¥<x<0)
U(x)=0,
в области
II
(0<x<¥)
U(x)=const=U0.
Различие в
U(x)
при переходе из области
I
в область
II
создает потенциальный барьер высотой
U0.
Решаем задачу о движении
микрочастицы через потенциальный барьер, используя уравнение
Шредингера.
Решение уравнения Шредингера
для области движения частицы до барьера (область
I)
будет:
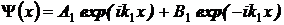 ,
,
где
A1
- амплитуда падающей на барьер волны,
B1
- амплитуда
отраженной от барьера волны,
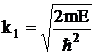 .
.
Отношение: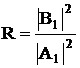 -
представляет собой коэффициент отражения
-
представляет собой коэффициент отражения
микрочастицы от
барьера.
Для области движения частицы
за барьером (область
II)
необходимо рассматривать 2 случая:
1.
E>U0
Частица, подчиняющая законам
классической механики, обязательно перейдет из области
I
область
II.
Микрочастица, для которой существенны волновые свойства,
должна вести себя иначе. При прохождении микрочастицы через
потенциальный барьер меняется ее кинетическая энергия, а
значит, меняется ее импульс и, следовательно, длина волны де
Бройля и скорость частицы. При переходе из области
I
в область
II
микрочастица имеет определенную вероятность отразиться и
определенную вероятность пройти дальше в область
II.
Итак, при
E>U0
решение уравнения Шредингера примет вид:
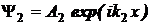 ,
,
где
A2
- амплитуда
прошедшей волны,
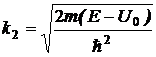 .
.
Коэффициент прозрачности
барьера определяется так:
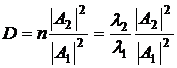 ,
,
где
l1,
l2
- длины волн де Бройля в области
I
и II.
2.
E<U0
По законам классической
механике переход из области
I
в область
II
невозможен.
Решение уравнения Шредингера
в области
II
для движущейся вдоль оси
х микрочастицы имеет вид:
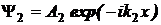 ,
,
где
A2
- амплитуда прошедшей волны.
Коэффициент отражения
частицы от барьера:
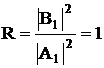 т.е
при E<U0
т.е
при E<U0
отражение является полным. Однако, вероятность обнаружения
частицы в области
II
не равна нулю:
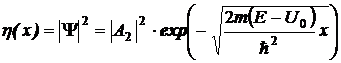 .
.
Наличие отличной от нуля
вероятности найти частицу в области за барьером на некоторой
глубине
x
делает возможным прохождение микрочастицы сквозь
потенциальный барьер конечной ширины. Такое прохождение
микрочастицы через потенциальный барьер получило название
туннельного эффекта. Оно является специфическим лишь для
квантовой механики и не имеет смысла в классической физике.
Коэффициент прохождения
D
потенциального барьера высотой
U0
и шириной
a
для микрочастицы массой
m
с энергией
E
может быть найден так:
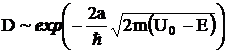 .
.

Под оператором
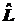 будем
понимать символ, показывающий, каким способом каждой из
рассматриваемого класса функций
U(X)
сопоставляется другая функция
V(X).
Это записывается так:
будем
понимать символ, показывающий, каким способом каждой из
рассматриваемого класса функций
U(X)
сопоставляется другая функция
V(X).
Это записывается так:
V (X)=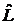 U(X),
U(X),
где
X
- обобщенная координата.
Оператор
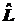 называется
линейным, если выполняются следующие соотношения:
называется
линейным, если выполняются следующие соотношения:
 ,
,
 ,
,
где
c1,
c2-
любые комплексные числа,
U1,
U2
- две
произвольные функции.

 Линейный
оператор
Линейный
оператор  называется
самосопряженным или эрмитовским, если выполняется равенство:
называется
самосопряженным или эрмитовским, если выполняется равенство:
 ,
,
где
 -
оператор комплексно сопряженный оператору
-
оператор комплексно сопряженный оператору
 .
.
Интегрирование производится
по всей области независимых переменных, совокупность
дифференциалов которых обозначена через
dX.
Действия над операторами
Рассмотрим два линейных
самосопряженных оператора
 и
и
 .
.
Суммой операторов
 и
и
 является
оператор
является
оператор  ,
если
,
если  .
Если
.
Если  ,
то
,
то  -
разность операторов.
-
разность операторов.
Произведением оператора
 на
постоянное число
c
, т.е. оператор
на
постоянное число
c
, т.е. оператор  ,
есть оператор, который умножает на
c
результат действия
,
есть оператор, который умножает на
c
результат действия
 на
Y:
на
Y:
 .
.
Алгебраические свойства
суммы и разности операторов аналогичны свойствам суммы и
разности чисел – операторы можно группировать, изменяя их
порядок записи.
Под произведением операторов
 и
и
 будем
понимать такой оператор
будем
понимать такой оператор
 ,
который, действуя на функцию
Y, переводит ее в
функцию, получаемую также путем последовательного применения
операторов сомножителей:
,
который, действуя на функцию
Y, переводит ее в
функцию, получаемую также путем последовательного применения
операторов сомножителей:
 .
.
Если
 ,
то операторы называются некоммутирующими, а если
,
то операторы называются некоммутирующими, а если
 ,
то операторы называются коммутирующими.
,
то операторы называются коммутирующими.
Для некоммутирующих
операторов  и
и
 -
коммутатор операторов
-
коммутатор операторов
 и
и
 .
.
Если операторы
 и
и
 являются
эрмитовскими, то произведение операторов
являются
эрмитовскими, то произведение операторов
 также
будет эрмитовским, если операторы
также
будет эрмитовским, если операторы
 и
и
 коммутируют,
т.е.
коммутируют,
т.е.  .
.
Уравнение:
 ,
,
является уравнением на
собственные функции оператора
 .
Решение этого уравнения позволяет найти собственные функции
оператора и спектр собственных значений. Собственные
значения эрмитовских операторов являются действительными
числами.
.
Решение этого уравнения позволяет найти собственные функции
оператора и спектр собственных значений. Собственные
значения эрмитовских операторов являются действительными
числами.

Постулаты квантовой
механики:
·
Каждой
физической величине
A
(координате,
импульсу, энергии, и т.д.) сопоставляется некоторый
эрмитовский оператор
 ,
действующий в квадратично – интегрируемом пространстве
L2.
,
действующий в квадратично – интегрируемом пространстве
L2.
·
Физическая
величина
A
в любом квантово-механическом состоянии может принимать
только те значения, которые принадлежат спектру ее оператора
 .
.
·
Среднее
значение физической величины
A
в состоянии, описываемом волновой функцией
Y(X)=Y(x,
y,
z,
t),
вычисляется по формуле:
 .
.
Операторы физических величин
Между операторами физических
величин существуют такие же соотношения, какие имеют место
между физическими величинами в классической физике.
Оператор координаты
совпадает с самой координатой, т.е. в координатном
представлении оператор координаты есть оператор умножения на
независимую переменную, т.е.
 ,
,
 .
.
Аналогично для координат
y
и z.
Оператором импульса
 в
координатном представлении является оператор
в
координатном представлении является оператор
 ,
где
,
где  .
.
Операторы проекций импульса
на оси координат:
 ,
,
 ,
,
 .
.
Оператор Гамильтона или
гамильтониан связан с операторами импульсов и координат
соотношением:
 ,
,
где
 ,
тогда
,
тогда  будет:
будет:
 .
.
Необходимым и достаточным
условием одновременной измеримости двух физических величин
является коммутация соответствующих операторов.
Операторы проекций момента
импульса:





Для решения ряда задач
используется оператор проекции момента импульса
 и
и
 в
сферических координатах:
в
сферических координатах:
 ,
,
где
 -
угловая часть оператора Лапласа.
-
угловая часть оператора Лапласа.

ИНТЕГРАЛЫ ДВИЖЕНИЯ.
Скорость изменения среднего
значения физической величины
A:
 (1),
(1),
где
 -
оператор скорости изменения физической величины, равный:
-
оператор скорости изменения физической величины, равный:
 (2).
(2).
В этом выражении
 -
оператор физической величины,
-
оператор физической величины,
 -
оператор Гамильтона.
-
оператор Гамильтона.
Из формулы (1) и (2)
следует, что среднее значение физической величины
сохраняется во времени в любом состоянии
Y, если:
·
 ,
т.е. оператор физической величины
A
явно от времени не
,
т.е. оператор физической величины
A
явно от времени не
зависит.
·
 ,
т.е.
,
т.е.  коммутирует
с гамильтонианом системы.
коммутирует
с гамильтонианом системы.
Физические величины, для
которых выполняются эти условия, называются сохраняющимися
или интегралами движения для данной системы.
Операторы большинства
физических величин ( )
явно от времени не зависят, а значит для них условие
сохранения физической величины
A,
представленной оператором, сводится к требованию
коммутативности
)
явно от времени не зависят, а значит для них условие
сохранения физической величины
A,
представленной оператором, сводится к требованию
коммутативности  и
и
 .
.
Вид оператора Гамильтона в
сферических координатах:
 ,
,
где
Ñ2
- оператор Лапласа в сферических координатах:
 (3),
(3),
в (3)
Ñr2-
радиальная часть оператора Лапласа, равная:
 ,
,
Ñq,j2-
угловая часть оператора Лапласа.

7.
ЛИНЕЙНЫЙ ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
Задача об одномерном
гармоническом осцилляторе сводится к решению уравнения:
 (1),
(1),
где
Y(x)
- волновая функция,
m
- масса,
E
- полная энергия гармонического осциллятора,
w
- частота гармонического осциллятора.
Путем замены переменных
 ,
,
 ,
,
 ,
,

уравнение (1) преобразуется
к виду:
 (2).
(2).
Уравнение (2) имеет
конечное, однозначное непрерывное решение, только при
определенных значениях параметра
e=2n+1,
где n=0,1,2….
Решение (2) выражается через
полиномы Эрмита:
 ,
,
где
 .
.
Для первых двух состояний (n
= 0,1) волновые функции имеют вид:
 ,
,
 .
.
Каждому состоянию,
изображаемому волновой функцией
Y(x)
соответствует одно значение энергии:
 ,
,
где
n
= 0,1,2….
Используемый при решении
задач табличный интеграл:
 xnexp(-x2)dx=
xnexp(-x2)dx= .
.

Собственные значения и
собственные функции оператора квадрата момента импульса
 следующие:
следующие:
M2=l(l+1)h2,
где
 l=0,1,2,…
- орбитальное квантовое число.
l=0,1,2,…
- орбитальное квантовое число.
 ,
,
где
m=0,±1,±2,…±l.
Функции
 для
s=(l=0)-,
p(s=1)
состояний приведены в таблице1 (с точностью до
нормировочного множителя).
для
s=(l=0)-,
p(s=1)
состояний приведены в таблице1 (с точностью до
нормировочного множителя).
Таблица 1
|
Состояние |
l,
m |
Ul,
m(q,j) |
|
s |
0,0 |
1 |
|
p |
1,0
1,1 |
cosq
sinq×exp(ij) |
Уравнение Шредингера для
стационарных состояний водородоподобных атомов в сферических
координатах
r,
q,
j
расщепляется на два
уравнения:
для радиальной части
R(r)
и угловой части
U(q,
j);
волновой функции
R(r)
в кулоновском
поле
U(r):
 .
.
Решения (собственные
функции)
R(r)
- радиального уравнения, позволяющие вычислить плотность
вероятности
wn(r)
нахождения электрона на расстоянии
r
от ядра

могут быть выражены через
полиномы Лагерра:
 ,
,
где
k=1,2…
- степень полинома, а
 -
обобщенное расстояние,
-
обобщенное расстояние,
выраженное через главное квантовое
число
n=1,2…
и радиус первой боровской орбиты
r1.
Функции
R(r)
для водородоподобных систем приведены в таблице 2
(с точностью до нормировочного множителя).
Таблица
2
|
Состояние |
n,
l |
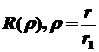 |
|
 |
1,0 |
exp(-r) |
|
 |
2,0 |
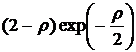 |
|
2p |
2,1 |
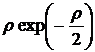 |
Используемый при решении
задач табличный интеграл:
 xnexp(-x)dx=
xnexp(-x)dx= .
.
